Knotenpotentialverfahren
In diesem Beitrag stellen wir dir das Knotenpotentialverfahren vor. Wir zeigen dir Schritt für Schritt, wie du die nötigen Gleichungen bestimmst und daraus eine Matrix erstellst, um schließlich alle Ströme und Spannungen deiner Schaltung zu erhalten.
Schau auch gerne in unser Video dazu rein, in dem wir es dir an einem Beispiel demonstrieren.
Inhaltsübersicht
Knotenpotentialverfahren einfach erklärt
Bei dem Knotenpotentialverfahren, handelt es sich um eine Methode mit der du sämtliche Ströme und Spannungen in einer Schaltung bestimmen kannst.
Hier siehst du eine Übersicht wie du beim Knotenpotentialverfahren vorgehen muss. Auf die einzelnen Schritte gehen wir anschließend anhand eines Beispiels genauer ein.
- Spannungsquellen in Stromquellen umwandeln: Falls in deinem Netzwerk Spannungsquellen vorkommen, dann musst du diese in eine passende Stromquelle umwandeln.
- Bestimmen sämtlicher Knoten: Die Knoten befinden sich immer an Verzweigungen deiner Schaltung, also wenn sich der Strom aufteilt oder ein neuer Strom dazu fließt.
- Ab- und zufließende externe Ströme eintragen: Hier betrachtest du nur die externen Ströme, die von außen in deine Schaltung hinein- oder herausfließen.
- Umwandeln aller Widerstände in Leitwerte: Der Leitwert G ist der Kehrwert des Widerstandes R, also G ist gleich eins durch R.
-
Aufstellen der Matrix nach folgendem Schema:
- die Diagonalelemente sind immer die negative Summe der Leitwerte, die mit dem jeweiligen Knoten verbunden sind.
- alle weiteren Matrixelemente entsprechen dem Leitwert, der die jeweiligen Knoten miteinander verbindet.
-
Bestimmung der Spannungen: Die Berechnung der Spannungen
 mit der Cramerschen Regel
oder dem Gaußschen Eliminationsverfahren
ist der letzte Schritt. Falls du das noch nicht kannst, dann schau dir unser Video dazu an.
mit der Cramerschen Regel
oder dem Gaußschen Eliminationsverfahren
ist der letzte Schritt. Falls du das noch nicht kannst, dann schau dir unser Video dazu an.
Knotenpotentiale
Wie der Name verrät, dreht sich beim Knotenpotentialverfahren alles um Knotenpotentiale. Ihre Definition lautet: Knotenpotentiale sind die Potentiale, also die Spannungen an allen Knoten. Dabei ist wichtig, dass das Potential an einem Knoten als Referenz genutzt wird. In anderen Worten: wir definieren diesen Knoten als Masse und setzen sein Potential zu Null.
Für jeden Knoten lässt sich nun die jeweilige Knotengleichung aufstellen. Zur Erinnerung:
Die Summe aller Ströme an einem Knoten ist gleich Null. Dabei geben wir dem in den Knoten zufließenden Strom ein negatives, dem abfließenden Strom ein positives Vorzeichen. Das nehmen wir aber nur in diesem Video als Vorschrift. Prinzipiell kannst du die Vorzeichen auch anders herum wählen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Knotenpotentialverfahren anwenden
Wie beim Maschenstromverfahren möchten wir beim Knotenpotentialverfahren am Ende ein Gleichungssystem aufstellen, das wir lösen können, um daraus die unbekannten Größen einer Schaltung zu bestimmen. Dabei gehen wir Schritt für Schritt vor.
Schauen wir uns folgenden Ausschnitt einer Schaltung mit den unbekannten Spannungen  ,
,  ,
,  und
und  doch mal genauer an.
doch mal genauer an.
Umwandlung von Spannungsquellen in Stromquellen
Als Erstes musst du beim Knotenpotentialverfahren alle Spannungsquellen in Stromquellen umwandeln. Dazu bestimmst die äquivalente Stromquelle zu den jeweiligen Spannungsquellen. Wie genau das funktioniert kannst du dir in unserem Video zu äquivalenten Strom und Spannungsquellen anschauen. In unserem Beispiel befinden sich keine Strom -und keine Spannungsquellen. Daher können wir diesen Schritt überspringen.
Bestimmung der Stromrichtungen
Als nächsten Schritt beim Knotenpotentialverfahren musst du alle Ströme, die in die Knoten zu- und abfließen mit entsprechendem Vorzeichen eintragen. Der entscheidende Part in diesem Verfahren ist nun, dass die inneren Ströme im Netzwerk mit Hilfe des Ohmschen Gesetzes.

durch die jeweiligen Spannungen ausgedrückt werden.
Diese Spannungen sind die Potentialdifferenzen zwischen den Knotenpotentialen  ,
,  ,
,  und
und  .
.
Aufstellen der Matrix
Jetzt kannst du damit beginnen die Matrix zur Bestimmung der gesuchten Spannungen aufzustellen.
Die inneren Ströme sind die Ströme, die innerhalb des Netzwerks zwischen den Knoten fließen. Ihre Bezeichnung wurde so gewählt, dass die erste Ziffer angibt an welchem Knoten er fließt. Die zweite Ziffer bezieht sich auf den Leitwert.
Am Knoten 4 gilt also beispielsweise:
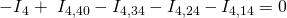
Das Vorzeichen der inneren Ströme kannst du beliebig wählen, da es von den jeweiligen Spannungen abhängt. Es bietet sich an sich an den Vorzeichen des Stromes der eingezeichneten Pfeile zu richten. Falls der reale Strom in die andere Richtung fließt, dann äußert sich das in einem negativen Vorzeichen.
Der Strom  kann mit Hilfe der Knotenpotentiale also folgendermaßen beschrieben werden:
kann mit Hilfe der Knotenpotentiale also folgendermaßen beschrieben werden:
![Rendered by QuickLaTeX.com I_4=\ U_4 \cdot G_{40}-{[U}_3-U_4] \cdot G34-[U2-U4] \cdot G24 - [U1-U4] \cdot G14](https://blog.assets.staging.studyflix.makandra.cloud/wp-content/ql-cache/quicklatex.com-62ab139e42180de3a4dcdba427f38a32_l3.png)
beziehungsweise aufgelöst ist dann

In dieser Form kannst du nun alle Ströme beschreiben. Übersichtlicher ist es, wenn du deine Gleichungen in einer tabellarischen Form aufschreibst. Dies sieht dann zum Beispiel so aus:
Vor allem hilft diese Schreibweise, wenn du dir dein Ziel noch einmal vor Augen führst. Am Ende des Knotenpotentialverfahrens möchtest du doch ein Gleichungssystem, also eine Matrix-Vektor-Gleichung, folgender Form erhalten, aus welcher du vergleichsweise einfach mit Hilfe der Cramerschen Regel die Spannungen berechnen kannst.
Wie du siehst, hast du also damit bereits deine Matrix aufgestellt.
Allgemeines Bildungsgesetz der Matrix
Für die Matrix bei dem Knotenpotentialverfahren gibt es ein allgemeines Bildungsgesetz. Das heißt: bei der Berechnung stellt man nicht alle einzelnen Knotengleichungen auf, sondern geht nach einem ganz einfachen Schema vor.
Schauen wir dazu nochmal auf unsere Schaltung und auf unsere fertige Matrix:
Wenn du dir klar machst, dass die Indizes auf die jeweiligen Knoten verweisen, dann kannst du zwei Dinge erkennen.
Die Diagonalelemente sind immer gerade die negative Summe aller Leitwerte, die mit dem jeweiligen Knoten verbunden sind. Die erste Zeile der Matrix bezieht sich auf Knoten 1.
Verbunden mit dem ersten Knoten sind die Leitwerte  ,
,  und
und  . Das Gleiche gilt auch für Zeile 2. Verbunden mit dem zweiten Knoten sind
. Das Gleiche gilt auch für Zeile 2. Verbunden mit dem zweiten Knoten sind  ,
,  ,
,  plus
plus  . Wenn du auf dem dritten Knoten stehst dann siehst du
. Wenn du auf dem dritten Knoten stehst dann siehst du  ,
,  und
und  . Jetzt bis du an der Reihe. Das Diagonalelement in Knoten vier kannst du jetzt ganz einfach alleine bestimmen. Jetzt fasst du alle Leitwerte in eine große Klammer und schreibst ein Minus davor.
. Jetzt bis du an der Reihe. Das Diagonalelement in Knoten vier kannst du jetzt ganz einfach alleine bestimmen. Jetzt fasst du alle Leitwerte in eine große Klammer und schreibst ein Minus davor.
Alle anderen Elemente in der Matrix entsprechen gerade dem Leitwert, der die jeweiligen Knoten miteinander verbindet. Die Matrix hat also genau soviel Zeilen wie Spalten.  verbindet die Knoten eins und zwei. Daher steht dieser in Zeile eins in der zweiten Spalte. Knoten 1 und 3 haben keine direkte Verbindung, daher bleibt die dritte Spalte in der ersten Zeile leer. Die Verbindungselemente bekommen immer ein positives Vorzeichen. Die Zeilennummer und Spaltennummer gibt an welche Knoten sie miteinander verbinden. Falls es keine direkte Verbindungen gibt, dann ist der Wert Null. Verbindungen über andere Knoten gelten nicht.
verbindet die Knoten eins und zwei. Daher steht dieser in Zeile eins in der zweiten Spalte. Knoten 1 und 3 haben keine direkte Verbindung, daher bleibt die dritte Spalte in der ersten Zeile leer. Die Verbindungselemente bekommen immer ein positives Vorzeichen. Die Zeilennummer und Spaltennummer gibt an welche Knoten sie miteinander verbinden. Falls es keine direkte Verbindungen gibt, dann ist der Wert Null. Verbindungen über andere Knoten gelten nicht.






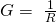 . Setzen wir das in das Ohmsche Gesetz ein, so ergibt sich:
. Setzen wir das in das Ohmsche Gesetz ein, so ergibt sich:






