Zweigstromanalyse
In diesem Artikel stellen wir dir die Zweigstromanalyse genauer vor. Dabei handelt es sich um ein Verfahren zur Bestimmung aller Ströme einer elektrischen Schaltung. Wir zeigen dir hier wie du dabei vorgehst und wann es sinnvoll ist mit der Zweigstromanalyse zu arbeiten.
Wenn du dir dazu einen Überblick verschaffen möchtest, schau doch gerne in unser Video rein.
Inhaltsübersicht
Zweigstromanalyse einfach erklärt
Die Zweigstromanalyse ist ein Verfahren zur Bestimmung aller unbekannten Ströme in einer Schaltung. Ihre Grundlage stellen die Kirchhoffschen Regeln dar. Sie helfen dir dabei die benötigten Knoten- und Maschengleichungen aufzustellen.
Das Vorgehen bei der Zweigstromanalyse besteht dabei aus fünf Schritten:
- Strom- und Spannungspfeile einzeichnen
- Knotenpunkte und Maschenumläufe einzeichnen
- Alle linear unabhängigen Knotengleichungen aufstellen
- Alle linear unabhängigen Maschengleichungen aufstellen und
- Gleichungssystem nach den Zweigströmen auflösen
Im Folgenden zeigen wir dir detailliert wie genau du bei den einzelnen Schritten vorgehen musst.
Zweigstromanalyse Beispiel
Um das Vorgehen bei der Zweigstromanalyse besser nachvollziehen zu können, wird folgende Beispielschaltung betrachtet:
Die Schaltung besteht aus den zwei Spannungsquellen 
und 
und den Widerständen 
, 
und 
.
Die Zweigstromanalyse basiert auf den Kirchhoffschen Regeln. Du wirst also Knoten -und Maschengleichungen aufstellen müssen.
Strom- und Spannungspfeile einzeichnen
Beim ersten Schritt, dem Einzeichnen der Strom und Spannungspfeile ist die Richtung frei wählbar. Üblicherweise zeigen Ströme und die zugehörigen Spannungspfeile in die gleiche Richtung.
Außerdem wird angenommen, dass der Strom aus der jeweiligen Spannungsquelle herausfließt. Dieser zeigt daher entgegengesetzt zur jeweiligen Quellenspannung. Die Zweigströme 
und 
fließen dementsprechend nach oben aus der Quelle heraus. Die Ströme und Spannungen benennst du üblicherweise nach den Widerständen. Zum Beispiel heißt der Strom durch den Widerstand .
Zudem fließen die Ströme und 
. Weiterhin fallen über den einzelnen Widerständen die Spannungen 
, 
und 
ab.
Knotenpunkte bestimmen
Als nächstes zeichnest du die Knotenpunkte und Maschenumläufe ein. Knotenpunkte kommen an alle Verzweigungen. An diesen kommt ein neuer Strom hinzu oder der Strom teilt sich auf. In unserem Beispiel bildet sich ein neuer Strom aus der Addition der Zweigströmen und .
Maschenumläufe
Im nächsten Schritt der Zweigstromanalyse zeichnest du die Maschenumläufe ein. In unserer Schaltung sind die beiden Maschen 
und 
direkt ersichtlich. Außerdem ist es für diese Schaltung nicht sinnvoll weitere Maschen aufzustellen, da diese von und linear abhängig wären. Maschen sind dann voneinander linear abhängig, wenn sich eine Maschengleichung durch Addition aus Vielfachen der anderen Maschengleichungen ergibt. Grundsätzlich solltest du dir merken, dass du beim Aufstellen der Maschen darauf achten musst, dass jede Spannung und damit jeden Bauteil mindestens einmal vorkommt. Bauteile dürfen allerdings auch in mehreren Maschen vorkommen: Der Widerstand kommt sowohl in Masche 
, als auch in 
vor. Wie du linear unabhängige Maschen bei komplexeren Schaltungen wählst, kannst du dir in unserem Video dazu anschauen.
Knotengleichungen aufstellen
Als dritten Schritt stellst du alle linear unabhängigen Knotengleichungen auf. In der Regel gibt es dabei eine Knotengleichung weniger als die Anzahl der Knoten. Die Knotengleichungen findest du durch Anwendung der ersten Kirchhoffschen Regel. Dieses besagt, dass die Summe aller Ströme an einem Knoten Null ist. Zudem gilt: Zeigt der Strompfeil zum Knoten hin, dann ist der Strom positiv. Kommt der Strom aus dem Knoten hinaus, dann ist sein Vorzeichen negativ.
Für die Knotengleichungen betrachten wir nur die einzelnen Ströme. Hier gilt:
In dieser Gleichung steckt keine neue Information, da sie ist linear abhängig mit der Gleichung für Knoten 1. Daher können wir die Gleichung für Knoten 2 vernachlässigen.
Maschengleichungen aufstellen
Schauen wir uns den nächsten Schritt der Zweigstromanalyse an: Hier musst du alle linear unabhängigen Maschengleichungen aufstellen.
Dazu gehen wir nach der zweiten Kirchhoffschen Regel vor: Die Summe aller Spannungen in einer Masche ist 0. Zeigen die Spannung und die Masche in die gleiche Richtung, dann ist das Vorzeichen der Spannung positiv, andernfalls ist das Vorzeichen negativ.
Für die Maschen gilt:
Hier berücksichtigen wir die Ströme, in dem wir die Spannungen , und mit 
ersetzen.
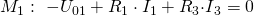
Auflösen des Gleichungssystems
Als letztes musst du nur noch das Gleichungssystem nach den Zweigströmen auflösen.
Unser Gleichungssystem sieht folgendermaßen aus:
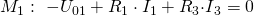
Nun hast du drei Unbekannte und drei Gleichungen. Durch geschicktes ineinander Einsetzen und Auflösen kannst du die Zweigströme , und bestimmen.
Aus 
folgt: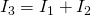 
Wenn du in die Maschengleichungen einsetzt und anschließendes nach auflöst, ergibt sich:
In Masche 2 setzen wir nun auch ein:
Jetzt setzen wir ein und lösen dann nach auf:
Das ergibt:
Wie du vielleicht gemerkt hast, ist dieser Schritt ziemlich aufwändig. Für zwei Maschen und ein Knoten ist er aber noch gut machbar und das schnellste Verfahren. Wenn deine Schaltung komplizierter wird, dann kannst du anstelle der Zweigstromanalyse das Knotenpunktpotentialverfahren oder das Maschenstromverfahren zu verwenden.