Video

KV-Diagramm

Du möchtest wissen, was das KV-Diagramm ist? Im Folgenden zeigen wir, wie du boolesche Funktionen einfach mit dem KV-Diagramm darstellen kannst.

Inhaltsübersicht

KV-Diagramm mit 4 Variablen vereinfachen – Minimierung von Funktionsgleichungen

Das KV-Diagramm wird auch als KVS-Diagramm, Karnaugh-Veitch-Diagramm, Karnaugh-Veitch-Symmetrie-Diagramm, KV-Tafel oder Karnaugh-Plan bezeichnet und wurde von Edward W. Veitch und Maurice Karnaugh entwickelt. Es dient dazu Boolesche Funktionen übersichtlich darzustellen, um sie anschließend zu minimieren. Mit Ihm ist eine Vereinfachung jeder logischen Funktion möglich. Das Diagramm besteht aus einer Zellenmatrix, bei der jeder Zelle eine bestimmte Kombination der möglichen Variablenwerte zugeordnet wird. Das Diagramm hat also 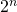2^n Felder, wobei n für die Anzahl der Variablen steht. Diese sind ähnlich dem Gray Code angeordnet.

KV-Diagramm

Schauen wir uns doch einmal ein solches Diagramm an. Wir haben hier 4 Variablen A, B, C und D. Das KVS-Diagramm hat somit 2^4 , also 16 Felder. Die Variablen werden an den Rändern mit Strichen aufgetragen. In dem Diagramm existiert von jeder Variable auch der negierte Wert. Beispielsweise sind die ersten beiden Zeilen der Bereich $\overline A$ , da A den Zeilen 3 und 4 entspricht. Dasselbe gilt auch für die anderen Variablen. Die Zahlen an den Rändern weisen jedem Kästchen eine bestimmte binäre Zahl zu. Diese Zahlen können auch in einer Wahrheitstabelle aufgereiht werden und entsprechen allen möglichen Kombinationen der Variablen A, B, C und D. Ihr realer Zahlenwert im Dezimalsystem findet sich in grün, links oben in den Zellen.

KV-Diagramm 3 Variablen

Je nachdem, wie viele Variablen verwendet werden, sieht das KV-Diagramm anders aus. Hier siehst du die Diagramme für 2 und 3 Variablen.

KV-Diagramm 3 Variablen — 2 und 3 Variablen

Wie können wir nun logische Funktionen mit dem KV-Diagramm am besten darstellen? Mit Hilfe eines einfachen Beispiels zeigen wir es dir.

KV-Diagramm Beispiel

Nehmen wir an, wir haben folgenden booleschen Ausdruck:

$\overline{B}C\overline{D}$

Nun wird in die Felder, auf die der Ausdruck zutrifft eine 1 eingetragen. Dies wird auch als Minterm der Funktion bezeichnet. Es gilt:

$m\left(X\right)=1\rightarrow F(X)=1$

X ist der Vektor der Eingangsvariablen. Alle anderen Felder erhalten eine 0. Wir haben hier einmal $\overline{B}$ , das entspricht der ersten und der vierten Reihe. C sind die letzten beiden Spalten des Diagrammes. Nun bleiben nur die zwei letzten Kästchen der ersten und der vierten Spalte übrig. Außerdem soll $\overline{D}$ zutreffen. Das KV-Diagramm für unseren Ausdruck sieht nun wie folgt aus:

KV-Diagramm Beispiel

Man kann das KV-Diagramm auch mit Hilfe der Wahrheitstabelle ausfüllen. Hier werden ebenfalls immer Einsen in die Felder eingetragen, wenn bei dem Output ein Minterm, also eine 1 vorliegt. Du weißt nun, wie KV-Diagramme aufgebaut sind und wie wir algebraische Begriffe eintragen können.

KV-Diagramm erstellen: Minterm eintragen

Nun kommen wir zur Vereinfachung. Nehmen wir diesmal einen komplizierteren algebraischen Ausdruck, um diese zu veranschaulichen. Du musst in folgenden vier Schritten vorgehen:

Zuerst trägst du die Minterms in dein KV-Diagramm ein.
Dann schaust du, ob sich bestimmte Anordnungen in dem Diagramm finden lassen.
Nun verknüpfst du die Einsen
Und schreibst zuletzt die neue boolesche Gleichung auf.

Wir gehen in der Funktionsgleichung von links nach rechts vor und tragen die Terme in das Diagramm ein.

KV-Diagramm erstellen — Minterm eintragen

Der erste Term ist , $\overline{B}$ , $\overline{C}$ und . A entspricht den unteren beiden Zeilen. $\overline{B}$ entspricht der oberen und der unteren Zeile, daher bleibt uns schon einmal nur die untere Zeile übrig. $\overline{C}$ entspricht den ersten beiden Spalten und D den zwei mittleren Spalten. Alles zusammengenommen bleibt uns also nur der orange markierte Kasten, da er sich im Schnittbereich der zweiten Spalte und der vierten Zeile befindet. Den ersten Teil der Funktionsgleichung haben wir damit erfolgreich verknüpft. Wir schreiben in Ihn eine 1 und machen mit den nächsten Begriffen weiter.

Vereinfachung: Zweier-, Vierer- und Achtergruppen

Nun vereinfachen wir. Es gibt im KVS-Diagramm verschiedene Einser-Gruppen, die algebraisch besonders einfach darzustellen sind. Diese sind benachbarte Zweier-, Vierer- und Achteranordnungen. Diese Gruppen können auch seitlich über das KV-Diagramm hinausgehen. Du musst dir dabei einfach vorstellen, dass du, sobald du rechts aus dem Karnaugh Diagramm kommst, bei den linken Feldern des KV-Diagramms wieder beginnst. Dasselbe gilt auch für oben und unten. Die Gruppen sind dann zwar nicht direkt benachbart, können aber trotzdem zusammengefasst werden.

KV-Diagramm Vereinfachung — Vereinfachung

Die Zweiergruppen reduzieren sich um 1 Variable, die Vierergruppen um 2 und die Achtergruppen um 3 Variablen. Wenden wir dies nun auf unsere Funktionsgleichung an.

Wenn wir unser Karnaugh Diagramm ansehen, können wir erkennen, dass wir zwei Vierergruppen haben. Diese können wir schon einmal als Funktionsgleichung aufschreiben. Wir erhalten:

$f(A,B,C,D)=\overline{C}$ $\overline{D}+$ $\overline{A}$ $\overline{D}$

Die linke Reihe lässt sich durch $\overline{C}$ und $\overline{D}$ beschreiben. $\overline{A}$ und $\overline{D}$ beziehen sich auf die obere Vierergruppe. Erinnere dich daran, dass wir gesagt haben, dass Gruppen auch über die Begrenzungen hinausreichen können. Nun fehlt nur noch ein einziger Minterm. Diesen beschreiben wir durch folgende Funktionsgleichung:

$f(A,B,C,D)=\overline{C}$ $\overline{D}+$ $\overline{A}$ $\overline{D}+$ $A\overline{B}$ $\overline{C}$

Um den Term möglichst simpel auszudrücken, wird er mit der 1 im linken unteren Eck gruppiert. Wie du siehst können Terme, um den algebraischen Ausdruck zu vereinfachen, auch mehrfach genannt werden.

Neben der soeben durchgeführten Minterm-Vereinfachung kannst du auch eine Maxterm-Vereinfachung vornehmen. Hier werden anstatt 1-er lediglich 0-en zusammengefasst. Du hast jetzt gelernt, wie du KV Diagramme aufstellen und sie für die Vereinfachung algebraischer Ausdrücke nutzen kannst. Wenn du das KV-Diagramm noch besser verstehen und anwenden willst, dann sieh dir doch unser Video zum Thema KV-Diagramm Übungen an. Hier gehen wir auch nochmal konkret auf die Wahrheitstabelle und die Verknüpfung der Einsen ein.

Beliebte Inhalte aus dem Bereich Digitaltechnik

Intro Digitaltechnik - Digitaler Schaltkreis

Boolesche Algebra

De Morgansche Gesetze

Boolesche Algebra vereinfachen

KV-Diagramm - Beispiel

Halb- und Volladdierer

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .