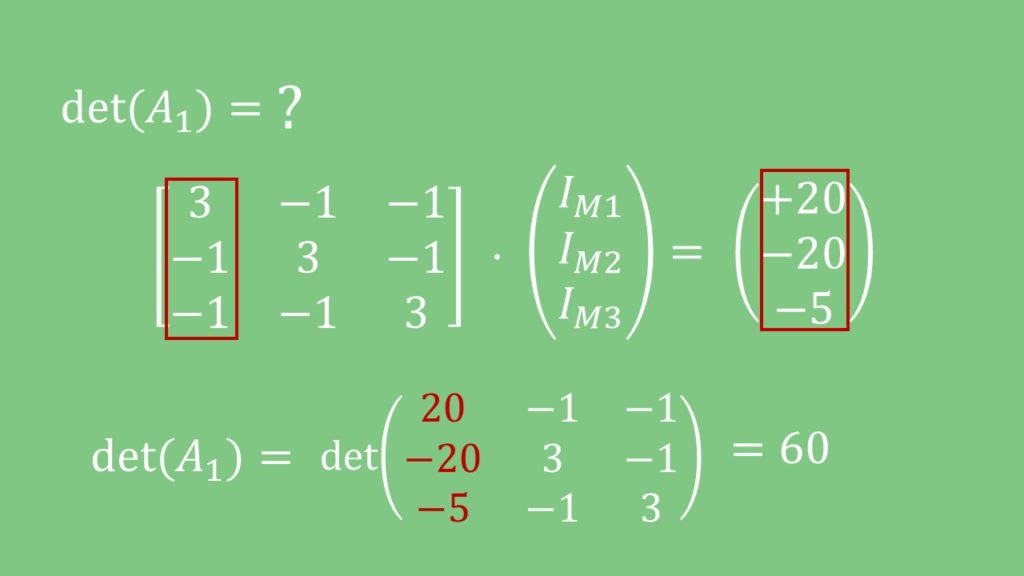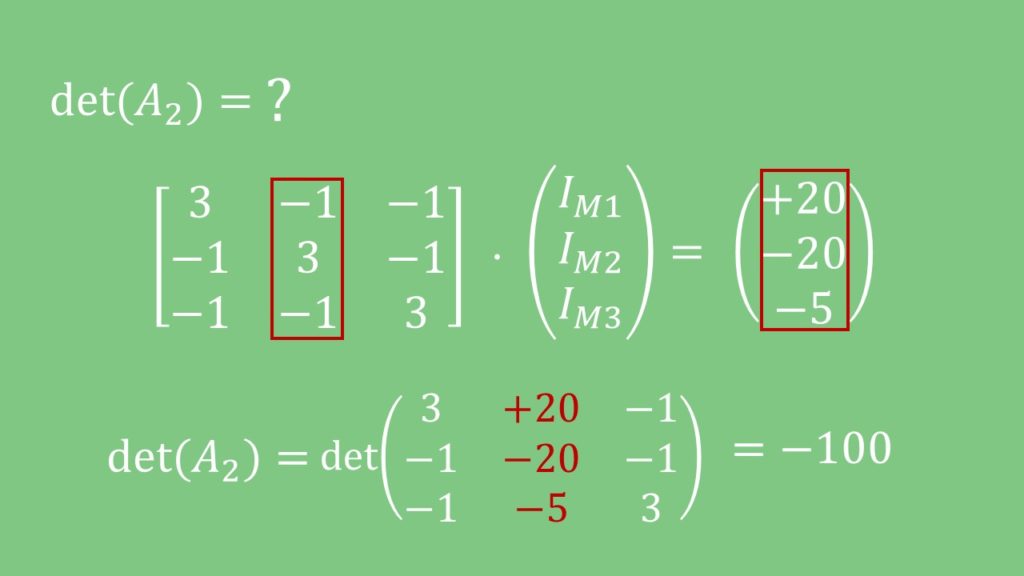Cramersche Regel
Dieser Artikel beschäftigt sich mich dem Lösen von Gleichungssystem mit der Cramerschen Regel. Wir zeigen dir wie du sie richtig anwendest und demonstrieren sie dir an einem Beispiel aus der Elektrotechnik.
Schau für eine Zusammenfassung auch gerne in unser Video dazu rein.
Inhaltsübersicht
Cramersche Regel einfach erklärt
Die Cramersche Regel ist ein Verfahren zur Bestimmung der Unbekannten eines linearen Gleichungssystems.
Ein lineares Gleichungssystem besteht allgemein aus einer Koeffizientenmatrix  , dem Variablenvektor
, dem Variablenvektor und dem Ergebnisvektor
und dem Ergebnisvektor  .
.
Die Cramersche Regel lässt sich in drei Schritte unterteilen:
- Bestimmen der Determinante
 der Matrix
der Matrix - Ersetzen der i-ten Spalte der Matrix mit dem Ergebnisvektor des Systems und Bestimmen der Determinanten

- Division der Determinanten
 durch die Determinante
durch die Determinante  zur Bestimmung der Unbekannten
zur Bestimmung der Unbekannten 
Anwendung der Cramerschen Regel
Bei der Cramerschen Regel handelt es sich um ein systematisches Verfahren zum Lösen von Gleichungssystem, das mit Determinanten arbeitet. Eine weitere Möglichkeit ist das Gaußsche Eliminationsverfahren .
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Berechnen der Determinanten A
Um ein Gleichungssystem mit der Cramerschen Regel zu lösen, musst du zuerst die Determinanten der Matrix bestimmen. Beispielsweise haben wir in den Gleichungssystemen der Maschenstrom- und Knotenpotentialverfahren eine 3×3 Matrix. Diese lässt sich mit der so genannten Regel von Sarrus, oder auch Zaunregel, berechnen.
Regel von Sarrus
Um die Regel von Sarrus anzuwenden, schreibst du am Besten die Matrix zwei Mal nebeneinander. Dann multiplizierst du alle Werte, die diagonal zueinander stehen. Die drei Terme, bei denen du oben startest, werden positiv und die Terme, bei denen du unten startest, negative berücksichtigt. So kannst du die Determinante  berechnen.
berechnen.

Berechnen der Unbekannten
Nachdem du jetzt deine Determinanten  , also
, also  ,
,  und
und  , kannst du deine Unbekannten
, kannst du deine Unbekannten  über folgende Formel bestimmen.
über folgende Formel bestimmen.

Gleichungssysteme in der Schaltungsanalyse
Wenn wir elektronische Schaltungen mit dem Maschenstrom– oder Knotenpunktpotentialverfahren analysieren, ergibt sich immer bei Gleichungssystemen aus n linearen Gleichungen mit n Unbekannten. Jedes System aus linearen Gleichungen lässt sich auch als Matrixgleichung schreiben.
Gleichungssystem mit der Cramerschen Regel lösen – Beispiel
Schauen wir uns das ganze mal an einem Beispiel für die Anwendung der Cramerschen Regel an. In unserem Beitrag zum Maschenstromverfahren kamen wir am Ende auf folgendes Gleichungssystem:
Gesucht sind die Maschenströme  ,
,  , und
, und  . Alle Wiederstände sind gleich groß und haben den Wert 1 Ohm. Die Spannungsquelle
. Alle Wiederstände sind gleich groß und haben den Wert 1 Ohm. Die Spannungsquelle  hat 5 Volt und die Quelle
hat 5 Volt und die Quelle  liefert 20 Volt. Wenn wir die Werte einsetzen, sieht unser Gleichungssystem folgendermaßen aus:
liefert 20 Volt. Wenn wir die Werte einsetzen, sieht unser Gleichungssystem folgendermaßen aus:
Zur besseren Übersicht, vernachlässigen wir im Folgenden die Einheiten.
Zuerst bestimmen wir die Determinante der Matrix  mit der Regel von Sarrus.
mit der Regel von Sarrus.
Im nächsten Schritt bilden wir die Matrix  , indem wir die erste Spalte der Matrix
, indem wir die erste Spalte der Matrix  durch den Ergebnisverktor ersetzen. Dann können wir mit Hilfe der Sarrus Regel auch die Determinante
durch den Ergebnisverktor ersetzen. Dann können wir mit Hilfe der Sarrus Regel auch die Determinante  berechnen.
berechnen.

Die Matrix  erhältst du, indem du die zweite Spalte von
erhältst du, indem du die zweite Spalte von  ersetzt.
ersetzt.

Anschließend ersetzen wir noch die dritte Spalte mit dem Ergebnisvektor und berechnen die Determinante  .
.

Jetzt hast du alle Werte, die du brauchst um mit der Cramerschen Regel deine Unbekannten also die Maschenströme zu berechnen:



An dieser Stelle ist es sinnvoll die Einheit  der Ströme wieder zu ergänzen.
der Ströme wieder zu ergänzen.