Du möchtest wissen, was ein XOR-Gatter ist? Im Folgenden zeigen wir dir, die Wahrheitstabelle, den booleschen Ausdruck und wie du es durch andere Gatter darstellen kannst.
Inhaltsübersicht
Kombinationen und Schaltsymbol
Wie beispielsweise auch das NAND- und das NOR-Gatter ist das XOR-Gatter eine Kombination aus den drei grundlegenden Logikfunktionen UND, ODER und NICHT.
Das XOR-Gatter wird auch als Exklusiv-Oder-Gatter und als Antivalenz Gatter bezeichnet. Im deutschsprachigen Raum sind für die Funktion folgende Symbole üblich.
Wahrheitstabelle und boolesche Ausdruck
Betrachte wir nun die zugehörige Wahrheitstabelle für unser Logikgatter.
Bei einem XOR-Gatter ist der Output nur 1, wenn eine ungerade Anzahl des Inputs auch 1 ist. Ist die Anzahl der Highs gerade, ist der Output 0. In der Booleschen Algebra wird die Funktion wie folgt dargestellt:
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
XOR-Gatter aus NAND
Wir können alle Gatter auch mit diesen beiden Funktionen darstellen. Das Schaltbild für eine äquivalente Schaltung für das XOR-Gatter, bestehend aus NAND-Gattern sieht beispielsweise so aus:
Hierbei werden drei NAND-Gatter zu einem XOR-Gatter zusammengeschlossen. Ob die beiden Gatter tatsächlich miteinander übereinstimmen, kannst du mithilfe einer Wahrheitstabelle prüfen. Wie du sehen kannst, hast du zunächst vier Inputs 
, 
, 
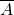und 
. Nicht A und Nicht B entsprechen in der Wahrheitstabelle jeweils dem Gegenwert von A und B. Also aus 1 wird 0 und umgekehrt. Nun folgen zwei NAND-Gatter, eines mit dem Input (Nicht A) und B und eines mit dem Input A und (Nicht B).
Für den Output 
des oberen NAND-Gatters musst du nun zuerst den Input miteinander malnehmen dann das Ergebnis umdrehen. Es ergibt sich nun: 1011. Algebraisch kannst du das auch so ausdrücken:
Versuche nun Output 
selbst aufzustellen. Kommst du auch auf folgendes Ergebnis? Die beiden Ergebnisse und dienen nun als Input für das letzte NAND-Gatter. Hier gehst du analog zum letzten Schritt vor. Wir nehmen die Inputs miteinander mal und drehen den Output um.
Wenn du das Ergebnis mit der Wahrheitstabelle für ein XOR-Gatter mit zwei Inputs vergleichst, wirst du sehen, dass der Output übereinstimmt. Alternativ kannst du die vier Inputs auch durch ein weiteres NAND-Gatter ersetzen.
Grundsätzlich kann man alle Gatter mit beliebiger Inputzahl durch NAND-Gatter darstellen, dies wird mit steigender Inputanzahl jedoch immer komplexer.
Du kennst nun das XOR-Gatter und kannst es auch durch NAND-Gatter darstellen. Außerdem haben wir unser Wissen über Wahrheitstabellen an einem Beispiel praktisch angewandt!
