Video

Freie Konvektion / natürliche Konvektion

Die natürliche Konvektion bereitet dir nach wie vor Sorgen und du möchtest endlich wissen, wie man die freie Konvektion berechnen kann? Dann lehn dich jetzt entspannt zurück, denn hier erklären wir dir kurz und präzise, was es mit der freien Konvektion auf sich hat.

Inhaltsübersicht

Die freie Konvektion anhand eines Alltagsbeispiels anschaulich erklärt

Den Trick, wie du ein Handtuch schneller trocknen kannst, kennst du bestimmt: Du musst es aufhängen, statt am Boden liegen zu lassen. Das Prinzip, das dahinter steckt, ist die natürliche Konvektion. Das Badetuch ist nass und somit kühler als die warme Umgebungsluft. Durch die Wärme kondensiert das Wasser im Handtuch und die Luft wird kühler. Die abgekühlte Luft strömt nach unten und warme Luft kommt oben wieder nach. Der Kreislauf ist also geschlossen. Das geht jetzt so lange, bis das Handtuch trocken ist. Die Luft kühlt deshalb nicht mehr ab, strömt nicht mehr nach unten und der Kreislauf verschwindet langsam. Dass das Handtuch also allmählich trocknet, hat einen Grund: die freie Konvektion.

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Freie Konvektion – Kreislauf

Freie Konvektion – Berechnungsarten

Wenn du nun genauer wissen willst, wie gut dein Handtuch die Wärme aus der Umgebung annimmt, dann musst du die freie Konvektion berechnen. Jedoch sollten wir zuerst noch klären, zu welcher Art unsere Berechnung zählt. Die Vorgehensweisen sind nämlich für vertikale Wände und Zylinder, geneigte Platten, horizontale Platten und horizontale Zylinder unterschiedlich.

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Freie Konvektion – Berechnungsarten

Da in unserem Fall das Badetuch an einer Leine hängt und somit vertikal ausgerichtet ist, musst du die Vorgehensweise der vertikalen Wände und Zylinder bei der Berechnung der natürlichen Konvektion anwenden.

Freie Konvektion berechnen – Beispiel Vertikale Wand

Zuallererst, um die freie Konvektion zu berechnen, musst du die Nusselt-Zahl bestimmen. Mit dieser kannst du dann den Wärmeübergang berechnen. Die Formel für Nu lautet:

$Nu=\left(0,825+\frac{0,387*{Ra}^\frac{1}{6}}{\left(1+\left(\frac{0,492}{Pr}\right)^\frac{9}{16}\right)^\frac{8}{27}}\right)^2$

Wie du die Prandtl-Zahl Pr berechnest, weißt du sicher schon, nämlich mit $Pr=\ \frac{\eta\ast cp}{\lambda}$ . Stellt sich nur noch die Frage, was Ra für eine Zahl ist. Das ist die sogenannte Rayleigh-Zahl und wird berechnet mit $Ra=Gr\ast Pr$ .

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Nusselt-Zahl, Prandtl-Zahl und Rayleigh-Zahl

Gr ist die Grashof-Zahl und wird in diesem Fall berechnet mit:

$Gr=\frac{g*\beta*H^3*\left(T_w-T_\infty\right)}{\nu^2}$

G ist dabei der Ortsfaktor und H die Platten- beziehungsweise Zylinderhöhe. $\beta$ beschreibt den volumetrischen, thermischen Ausdehnungskoeffizienten, der mit der Formel $\beta=\frac{1}{T_{bez}}$ berechnet wird. Die Bezugstemperatur in der Berechnung der freien Konvektion ist hier $T_{bez}=\frac{T_w+T_\infty}{2}$ .

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Grashof-Zahl

So, jetzt kannst du alle Komponenten bestimmen und damit die Nusselt-Zahl berechnen. Wie in all den Rechnungen zuvor, gilt auch hier wieder $Nu\ =\frac{\alpha\ast H}{\lambda}$ . Nach $\alpha$ umgestellt, lautet die Formel dann $\alpha=\frac{Nu\ast\lambda}{H}$ . Wenn dir in der Klausur jetzt die einzelnen Stoffgrößen gegeben sind, kannst du mit diesen Formeln berechnen, wie gut der Wärmeübergang im Verlauf der natürlichen Konvektion an deinem Badetuch ist.

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Nusselt-Zahl berechnen

Freie Konvektion berechnen – Beispiel Geneigte Platte

Aber sicherlich interessieren dich auch noch die anderen Fälle der freien Konvektion. Bei der geneigten Platte musst du lediglich die Grashof-Zahl anders berechnen. Denn dabei muss noch der Winkel, um den die Platte geneigt ist, miteingebracht werden, um die freie Konvektion berechnen zu können. Die Formel lautet dann:

$Gr=\frac{g*cos\gamma*\beta*H^3*\left(T_w-T_\infty\right)}{\nu^2}$

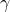$\gamma$ ist dabei der Neigungswinkel der Platte. Die restlichen Kennzahlen kannst du dann genauso berechnen, wie bei der natürlichen Konvektion der vertikalen Wände.

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Freie Konvektion berechnen – Geneigte Platte

Freie Konvektion berechnen – Beispiel Horizontale Platte

Bei den horizontalen Platten ändert sich in Bezug auf die freie Konvektion auch die Formel für die Nusselt-Zahl, da es darauf ankommt, wie die Plattenoberflächen jeweils erwärmt beziehungsweise gekühlt werden. Die Formel lautet ${Nu=x\ast Ra}^n$ , wobei x und n von der Rayleigh-Zahl abhängen. Für den Fall, dass die Plattenoberseite beheizt oder die Plattenunterseite gekühlt wird, ist x gleich 0,54 und n gleich 0,25 falls ${10}^4\le\ Ra\le{10}^7$ . x ist 0,15 und n ist 0,33, falls ${10}^7\le\ Ra\le{10}^{11}$ .

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Freie Konvektion berechnen – Horizontale Platte

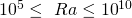Wenn wir den umgekehrten Fall haben, also dass die Plattenoberseite gekühlt, beziehungsweise die Plattenunterseite gewärmt wird, dann ist x gleich 0,52 und n gleich 0,20 falls ${10}^4\le\ Ra\le{10}^9$ ist. x ist 0,27 und n ist 0,25, falls ${10}^5\le\ Ra\le{10}^{10}$ . Die Rayleigh-Zahl berechnest du wieder mit $Ra=Gr\ast Pr$ . Allerdings ist bei der Grashof-Zahl dieses Mal die Bezugslänge nicht H, sondern L‘. L‘ ist das Verhältnis von wärmeabgebender Oberfläche zu äußerer Umrandung, also $L'=\frac{A}{U}$ . Somit lautet dann die Formel für die Grashof-Zahl:

$Gr=\frac{g*\beta*{L'}^3*\left(T_w-T_\infty\right)}{\nu^2}$

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Grashof-Zahl – Geneigte Platte

Mit diesen Größen kannst du dann die Nusselt-Zahl berechnen und somit auch den Wärmeübergang mit:

$\alpha=\frac{Nu\ast\lambda}{L\prime}$

Die Berechnung des Wärmeübergangkoeffizienten für horizontale Zylinder ist der der vertikalen Berechnung in Bezug auf die freie Konvektion wieder ähnlicher. Hier ändert sich auch erneut die Grashof-Zahl hinsichtlich der Bezugslänge. Statt H ist hier der Außendurchmesser D die richtige Größe, wodurch sich die Formel verändert zu:

$Gr=\frac{g*\beta*D^3*\left(T_w-T_\infty\right)}{\nu^2}$

Freie Konvektion, Natürliche Konvektion, Freie Konvektion berechnen — Freie Konvektion berechnen – Horizontaler Zylinder

Bei der Nusselt-Zahl ändern sich lediglich die Vorfaktoren, so dass sich für die Berechnung ergibt:

$Nu=\ \left(0,6+\frac{0,387*{Ra}^\frac{1}{6}}{\left(1+\left(\frac{0,559}{Pr}\right)^\frac{9}{16}\right)^\frac{8}{27}}\right)^2$

Wie du dir wahrscheinlich denken kannst, musst du auch für den Wärmeübergang wieder die passende Bezugslänge einsetzen. Dadurch kommst du dann mit $\alpha=\frac{Nu\ast\lambda}{D}$ auf deinen Wärmeübergangskoeffizienten.

Jetzt bist du umfassend über die natürliche Konvektion informiert und weißt auch, wie man die freie Konvektion berechnen kann.

Beliebte Inhalte aus dem Bereich Wärmeübertragung

Wärmeübertrager

Dauer: 06:56

Intro Wärmeübertragung

Stationäre Wärmeleitung

Instationäre Wärmeleitung

Konvektiver Wärmeübergang

Erzwungene Konvektion - Durchströmte Rohrleitung

Erzwungene Konvektion - längsumströmte, ebene Platte

Erzwungene Konvektion - Querumströmter Körper

Natürliche Konvektion

Wärmeübertrager

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .