Lineare Preis-Absatz-Funktion
Das Thema Preis-Absatz-Funktion ist für sehr viele verschiedene wirtschaftliche Themenbereiche relevant. Wir erklären dir die lineare und die multiplikativen Preis-Absatz-Funktion kurz und knapp an zwei Beispielen.
Du möchtest lieber hören statt lesen? Dann schau dir direkt unser Video an.
Inhaltsübersicht
Preis Absatz Funktion einfach erklärt
Die Preis-Absatz-Funktion (Preisabsatzfunktion), kurz PAF, wird eingesetzt, um den zu erwartenden Absatz bei einem bestimmten Preis zu ermitteln. Ziel ist es, den optimalen Preis und die daraus resultierenden optimalen Absatzmengen herauszufinden, bei denen der Deckungsbeitrag am größten ist. Die Preis-Absatz-Kurve kann, wie bereits oben erwähnt, verschiedene Verläufe aufweisen. In diesem Beitrag betrachten wir zunächst die lineare Preis-Absatz-Funktion und gehen dann weiter zur multiplikativen Preis-Absatz-Funktion.
Lineare Preis-Absatz-Funktion Formel
Zunächst möchten wir dir die lineare Preisabsatzfunktion näherbringen und betrachten daher die Preis-Absatz-Funktion Formel:
Der Parameter 
entspricht dabei dem Schnittpunkt der Funktion mit der y-Achse. Das ist der theoretisch maximale Absatz bei einem Preis von null und wird als Sättigungsmenge bezeichnet.
ist die Reaktion des Absatzes auf die Preisänderung und ist zugleich die Steigung der Preis-Absatz-Kurve. In der Regel ist die Steigung negativ, da bei einem steigenden Preis der Absatz abnimmt. Somit steigt der Absatz um den Wert bei einer Preissenkung um eine Einheit. Bei einer positiven Steigung, nimmt der Absatz bei einer Preiserhöhung ebenfalls zu.
Lineare Preis-Absatz-Funktion berechnen
Aber schauen wir uns doch mal die lineare Preis-Absatz-Funktion an einem Beispiel an. Stell dir vor, du arbeitest neben dem Studium im Kino um die Ecke. Dir fällt auf, dass es bisher keine Unterscheidung eurer Kunden in Studenten und Nicht-Studenten gibt. Dein Chef ist begeistert von der Idee und schlägt vor, dass du doch mal die optimalen Preise und die daraus resultierenden Absätze für die beiden Alternativen ermitteln kannst. Die variablen Kosten belaufen sich auf 18 Euro. Du nimmst an, dass eine lineare Preisabsatzfunktion vorliegt. Für Studenten lautet der Parameter 
und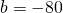 
. Bei Nicht-Studenten ist 
und 
.
Berechnung der Preis-Absatz Funktion: Studenten
Zuerst wollen wir die Studenten näher betrachten. Hierzu setzen wir erst einmal die uns bekannten Werte in die Funktion ein. Aus der Formel kannst du erkennen, dass bei einem Preis von Null, maximal 800 Karten verkauft werden können. Am Wert 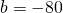siehst du, dass bei einer Preissteigerung um einen Euro, 80 Karten weniger abgesetzt werden können.
Nun verwenden wir die Preis-Absatz-Funktion der Studenten im Deckungsbeitrag. Um jetzt den optimalen Preis der Studenten zu errechnen, leiten wir den Deckungsbeitrag nach dem Preis ab und erhalten den für Studenten optimalen Preis von 7,5 Euro. Der Preis wird in die Preis-Absatz-Funktion Formel eingesetzt und ergibt einen Absatz von 200 Eintrittskarten.
Jetzt können wir noch den Gewinn durch die an Studenten verkauften Tickets berechnen. Wir kommen hierbei auf 500 Euro.
Berechnung der Preis-Absatz Funktion: Nicht-Studenten
Für die Gruppe der Nicht-Studenten müssen wir nun das Selbe machen. Dazu setzen wir die PAF in den Deckungsbeitrag ein und erhalten die Deckungsbeitragsformel: Diesen leiten wir wieder nach dem Preis ab und erhalten den optimalen Preis von 12,50
Bei diesem Preis wird ein Absatz von 225 Eintrittskarten erreicht und er führt zu einem Gewinn von 2187,5 Euro. Bei der Aufteilung kann also ein Gesamtgewinn von 2187,50 Euro erreicht werden.
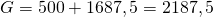
Um nun deinem Chef zu zeigen, ob sich die Aufteilung lohnt, müssen wir noch den Deckungsbeitrag ohne die Einteilung in Studenten und Nicht-Studenten berechnen. Hierzu kombinieren wir die einzelnen Funktionen zu einer Einzigen. Die neue PAF sieht dann so aus:
Die neue Funktion wird jetzt in den Deckungsbeitrag eingesetzt. Nun berechnen wir erneut den optimalen Preis und die daraus resultierende Absatzmenge. Der Preis beläuft sich auf 8,86 Euro und führt zu einem Absatz von 425,5 Eintrittskarten. Jetzt können wir erneut den Gewinn berechnen und kommen auf 1642 Euro.
Sehr gut! Wie du siehst ist der Gewinn mit einer Aufteilung in Studenten und Nicht-Studenten größer als ohne eine Aufteilung.
Zuletzt können wir noch den Nutzen für den Kinobetreiber berechnen und sehen, dass er durch eine Aufteilung eine Gewinnsteigerung von 545,5€ hat.
Super! Die Lineare-Preisabsatzfunktion sollte kein Problem mehr sein. Merk dir am besten ihre Funktion
dann bist du schon mal gut ausgerüstet.
Preis-Absatz-Funktion Monopol und Oligopol
Zum Schluss muss man noch beachten, dass wir die analytische Preis-Absatz-Funktion nur bei Preissetzern beziehungsweise Preisakteuren nutzen können. Ein Beispiel wäre hier die Monopolstellung, wenn wir also die einzigen Anbieter für ein Produkt auf dem Markt sind. Im Gegensatz dazu ist die PAF für Mengenanpasser nicht aussagekräftig. Das kommt daher, dass wir den Preis als Variable verwenden und ihn daher auch anpassen können müssen.
Im nächsten Abschnitt schauen wir uns noch die Multiplikative Preis-Absatz-Funktion an.
Multiplikative Preis-Absatz-Funktion
Die multiplikative Preis-Absatz-Funktion ist eine weitere Variante, mit der du den Bezug des Preises auf den Absatz ermitteln kannst. Sie hat einen anderen Verlauf als die lineare Preis-Absatz-Kurve und daher auch eine andere Preis-Absatz-Funktion Formel.
Multiplikative Preis-Absatz-Funktion Formel
Die multiplikative Preis-Absatz-Funktion Formel sieht wie folgt aus:
Der Parameter ist im Gegensatz zur linearen Preis-Absatz-Funktion nicht die Sättigungsmenge, sondern nur ein Normierungsparameter, der die Höhe des Absatzes bei einem Preis von 1 festlegt. Der Parameter steuert wie stark die Absatzmenge vom Preis abhängig ist. Das bedeutet, dass der Verlauf der Preis-Absatz-Kurve nur vom Wert abhängt. Umso höher der betragsmäßige Wert von ist, desto schneller nähert sich die multiplikative Preis-Absatz-Kurve an die x-Achse an.
Die absolute Wirkung der Preisänderung hängt vom Ausgangspreis 
ab. Je niedriger ist, desto stärker ist die Wirkung der Preisveränderung auf die Menge.
Multiplikative Preis-Absatz-Funktion Beispiel
Um die multiplikative Preis-Absatz-Funktion etwas besser zu verdeutlichen, schauen wir uns ein Preis-Absatz-Funktion Beispiel an. Stell dir vor, du hast ein Unternehmen und bietest dein Produkt als einziger auf dem Markt an. Die variablen Stückkosten belaufen sich auf 2,50 € und der optimale Deckungsbeitrag liegt bei 250 €. Die Preiselastizität der Nachfrage beträgt -2 und ist somit im preiselastischen Bereich. Du unterstellst, dass eine multiplikative Preis-Absatz-Funktion vorliegt.
Die Preiselastizität der multiplikativen Preis-Absatz-Funktion ist gleich dem Parameter . Somit ist der erste Wert mit -2 bereits ermittelt. Um nun den letzten fehlenden Parameter zu berechnen, wird es etwas aufwendiger. Zunächst lässt sich der optimale Preis bestimmen, indem wir die Deckungsbeitragsformel nach ableiten. Somit erhalten wir die Formel für den optimalen Preis:
Multiplikative Preis-Absatz-Funktion berechnen
Setzen wir jetzt die bereits bekannten Werte ein, erhalten wir den Wert 5€ als den optimalen Preis. Nun setzen wir die uns bekannten Werte in die Deckungsbeitragsformel ein. Dadurch bekommen wir den letzten fehlenden Parameter , der 2.500 beträgt. Jetzt haben wir alles, um die multiplikative Preis-Absatz-Funktion berechnen zu können.
Jetzt möchten wir dir noch die absolute Wirkung einer Preisänderung auf die Menge genauer zeigen. Dazu nehmen wir mal an, dass der Ausgangspreis gleich 5€ ist und wir die gerade ermittelte multiplikative Preis-Absatz-Funktion haben. Bei 5€ ist der Absatz gleich 100 Stück. Erhöhen wir nun den Preis auf 10€, sinkt der Absatz auf 25 Stück ab. Durch die Preiserhöhung von 5€ auf 10€ wird der Absatz also um 75 Stück gesenkt. Setzen wir den Ausgangspreis nun niedriger, zum Beispiel auf 2€, lässt sich ein Absatz von 625 Stück erzielen.
Erhöhen wir nun den Preis wiederum um 5 €, auf 7 €, so sinkt der Absatz auf 51 Stück ab. Der Absatz wird also um ganze 574 Stück vermindert. Dadurch kannst du sehen, dass eine Änderung des Preises umso stärker auf die Absatzmenge wirkt, je niedriger der Ausgangspreis ist.