AS AD Modell: Übung
Aufbauend auf die Videos zum AS AD Modell behandelt dieser Artikel eine Übungsaufgabe mit konkreten Berechnungen.
Die Theorie in Schriftform ist dir zu trocken? Dann sieh dir unser Video an und löse zusammen mit uns Schritt für Schritt die Übungsaufgabe zum AS AD Modell. Los geht’s!
Inhaltsübersicht
Aufstellen der AS und der AD Kurve anhand eines Beispiels
Nach all der trockenen Theorie in den letzten Videos, wollen wir das Gelernte jetzt endlich in der Praxis anwenden. Wir haben dir dafür eine kleine Übungsaufgabe vorbereitet. Die Form sieht dabei etwas anders aus, als in der Theorie, aber die Methode bleibt die Gleiche. Und damit auf ins Gefecht!
Gegeben sind uns folgende Zusammenhänge:
Herleitung der AD-Kurve
Die AS-Kurve ist uns also schon bekannt. Wir wollen uns deswegen noch die AD Kurve herleiten. Du erinnerst dich, dass sich diese aus der IS und der LM Kurve zusammensetzt. Schauen wir uns für unsere Herleitung doch noch einmal die Grundformen der entsprechenden Gleichungen an.
Die IS Kurve ergab sich zu:

Und die LM Kurve zu:
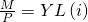
Fangen wir mit der IS Kurve an. Hier müssen wir einfach die gegebenen Gleichungen und Werte einsetzen, und erhalten:

Kürzen wir diese Gleichung und stellen sie nach i um, ergibt sich:


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Die LM Kurve
Um damit auf die AD Kurve zu kommen, benötigen wir noch eine vergleichbare Darstellung für die LM Kurve. Dafür werfen wir einen erneuten Blick in die Angaben und stellen fest: Uns wurde die LM Kurve in modifizierter Form bereits gegeben:

Lass dich davon nicht verwirren; die Angaben sind meist nicht ganz eindeutig. Wichtig ist, dass alle erforderten Parameter in der Gleichung vorkommen. Wir können diese nun ebenfalls nach i umstellen und erhalten:


Setzen wir die beiden Zusammenhänge für i nun gleich, folgt:



Super, damit haben wir auch schon unsere AD Kurve bestimmt. Nehmen wir an, dass außerdem das natürliche Produktionsniveau gegeben ist mit:

und die Geldmenge im Ausgangsgleichgewicht mit,

Dann können wir direkt das Preisniveau der mittleren Frist berechnen. Dafür setzen wir alle gegebenen Werte in die AD-Kurve ein und erhalten:


Betrachtung der mittleren Frist
Für die mittlere Frist gilt, dass bei natürlichem Produktionsniveau das erwartete Preisniveau dem tatsächlichen Preisniveau entspricht:

Den Zinssatz schließlich erhalten wir über einsetzen in die IS Gleichung:


Der Zinssatz beträgt also vier Prozent. Und damit haben wir auch schon die wichtigsten Werte unseres AS AD Modells bestimmt.
Und jetzt wird es spannend. Wir überlegen uns nämlich, was mit den Formeln passiert, wenn wir einen der Effekte aus den letzten beiden Videos annehmen: Die restriktive Geldpolitik. Restriktiv bedeutet, dass die nominale Geldmenge abnimmt; wir nehmen unser neues M für diese Rechnung also an zu:

Um die Aufgabe zu lösen, gehen wir außerdem von einer sogenannten adaptiven Erwartungsbildung aus. Das bedeutet, dass das erwartete Preisniveau in der folgenden Periode dem Preisniveau der aktuellen Periode entspricht. Für unsere Betrachtung erhalten wir damit:

Damit können wir für unsere AS Gleichung schreiben:


Doch eigentlich interessieren wir uns mehr für die AD Kurve, denn diese verschiebt sich ja am Ende durch die Veränderung der Geldmenge. Um AD‘ zu erhalten, ersetzen wir daher einfach in unserer AD Gleichung M durch M1:

Damit ergibt sich unsere neue Kurve zu:

Lösen wir diese nun nach Y1 auf:

Und setzen den Ausdruck der AS Kurve für P Eins ein, erhalten wir:



Das neue Preisniveau ergibt sich dann durch einsetzen in die AS-Kurve zu:

Damit haben wir jetzt das neue Gleichgewicht im ASAD Modell herausgefunden. Natürlich kannst du auch hier wieder den Zinssatz i berechnen, indem du die Werte für die erste Periode, in die IS oder die LM Gleichung einsetzt:




Der Zinssatz nach der Reduktion beträgt also circa 5,6%. Das Zinsniveau ist im Vergleich zum vorherigen Zustand gestiegen, die Produktion und auch das Preisniveau sind gesunken. Wir haben damit rechnerisch die Verschiebung der AD-Kurve bei einer restriktiven Geldpolitik belegt. Analog kannst du jetzt natürlich auch die anderen Effekte wie den expansiven Fall oder Angebotsschocks berechnen. Probier das doch einfach mal aus und ersetze einen der gegebenen Parameter durch einen größeren oder kleineren Wert!
