Video

Optimale Losgröße

Wichtige Inhalte in diesem Video

Optimale Losgröße einfach erklärt

Optimale Losgröße Beispiel

Von der optimalen Losgröße in der Losgrößenplanung hast du bereits gehört, aber weißt nicht wirklich was sich dahinter verbirgt und wie du diese Kennzahl berechnen kannst? Wir erklären dir in diesem Artikel alles, was du zur Berechnung der optimalen Losgröße wissen musst.

Du bist eher der audiovisuelle Typ? Dann schau dir direkt unser Video zur optimalen Losgröße an.

Inhaltsübersicht

Optimale Losgröße einfach erklärt

im Videozur Stelle im Video springen

Die optimale Losgröße bezeichnet die Menge an Produkten, die gesammelt produziert werden um die Produktionskosten (z.B. Lagerhaltungskosten und Rüstkosten) minimal zu halten. Mit Berechnung der optimalen Losgröße möchtest du also die kostengünstigste Losgröße ermitteln. Grundsätzlich gibt es zwei Aspekte, die ein Unternehmen bei der Kalkulation der optimalen Losgröße beachten muss:

Produziert das Unternehmen kleine Losgrößen, so sind die Lagerhaltungskosten ( Lagermiete, Personalkosten im Lager, …) eher gering. Allerdings sind dann die sogenannten Rüstkosten sehr hoch, da die Maschinen nach jedem (Produktions-)Los umgestellt bzw. umgerüstet werden müssen.
Wenn das Unternehmen hingegen große Lose hergestellt, so sind die Lagerhaltungskosten für die produzierten Menge höher, dafür aber die Rüstkosten für die Maschinen geringer.

Losgröße

Von einer Losgröße sprechen wir bei der Menge von Produkten oder einzelnen Produktteilen, die gesammelt produziert wird, bevor die Fertigungsmaschinen für andere Produkte bzw. Teile umgerüstet werden. Stellt ein Unternehmen beispielsweise 5.000 Karabinerhaken mit einer Größe von 3 cm im Zeitraum zwischen 7 und 13 Uhr her und anschließend von 14 bis 18 Uhr 3.000 Haken mit einer Größe von 5 cm, so sind die Mengen 5.000 und 3.000 jeweils eine Losgröße. In der Zeit zwischen 13 und 14 Uhr entsteht ein Produktionsstop, da die Maschinen auf die neue Größe der Produkte angepasst werden müssen. Dies verursacht dem Unternehmen sogenannte Rüstkosten.

Das spricht natürlich dafür, dass das Unternehmen möglichst große Lose produziert, damit sich diese Kosten auch lohnen. Andererseits müssen die produzierten Haken gelagert werden, was dem Unternehmen Lagerkosten und Kapitalbindungskosten verursacht. Es ist also Aufgabe der Losgrößenplanung, die optimale Losgrößen zu bestimmen, um diese Kosten so minimal wie möglich zu halten.

Optimale Losgröße berechnen

Bei der Losgrößenplanung geht es darum die optimale Losgröße herauszufinden. Diese sogenannte Planung der optimalen Losgröße ist eine Entscheidung, die auf kurze Frist getroffen wird. Die Formel für die Berechnung der optimale Losgröße wird auch als Andler Formel bezeichnet. Diese sieht folgendermaßen aus:

$q = \sqrt{\frac{2\cdot m \cdot k_B}{w \cdot (i_K + i_p_h)}}$ = $\sqrt{\frac{2 \cdot Jahresbedarf \cdot Bestellkosten}{Produktwert \cdot Lagerkostensatz}}$

Wir erklären dir die Andler Formel in unserem Video zur optimalen Bestellmenge nochmal genauer.

Optimale Losgröße Beispiel

im Videozur Stelle im Video springen

Schauen wir uns nun ein Bespiel zur optimalen Losgröße an. Im ersten Fall produzierst du diese nicht selbst, sondern beschaffst sie von einem externen Lieferanten. Dabei musst du planen wie viele Bänder du in welchen zeitlichen Abständen bestellen solltest. Es handelt sich in diesem Fall also um die Berechnung der optimalen Bestellmenge. In der Supply Chain befinden wir uns hier in der Phase der Beschaffung. Im zweiten Fall produzierst du die Armbänder selbst. Diese Situation schauen wir uns in einem separaten Video zur Optimalen Losgröße bei Eigenproduktion genauer an.

Optimale Losgröße bei Fremdbeschaffung: Optimale Bestellmenge

Bei der Fremdbeschaffung erfolgt die Bestellung bzw. Lieferung der Losgröße Q in konstanten Zeitabständen. Die Ware wird also zeitpunktgeballt geliefert. Die Lieferung erfolgt immer, wenn du deinen Sicherheitsbestand erreicht hast. Die Berechnung der Bestellmenge erfolgt nach dem sogenannten EOQ-Modell. Die entscheidende Frage beim EOQ Modell ist jetzt, wie groß das Los Q und wie lang der Bestellzyklus t sein muss, damit die Kosten minimal sind.

Bestellmenge berechnen

Die Formel für die Bestellmenge lautet:

$q=t\ \ast\ d$ bzw. $t=\frac{q}{d}$

Die Bedarfsrate d ist in der Regel gegeben. Du brauchst also noch eine weitere Variable, um die Formel zu berechnen. Hier bietet sich die Losgröße q an, da sie sich gut über die Kostenfunktion bestimmen lässt. Durch die optimale Losgröße q* kannst du dann auch den optimalen Bestellzyklus t* bestimmen. Schauen wir uns also die Kostenfunktion an.

Optimale Losgröße — Bestellmenge und Bestellzykluslänge

Kostenfunktion der optimalen Bestellmenge

Diese ergibt sich zum einen aus den Lagerkosten und zum anderen aus den bestellfixen Kosten. Die Lagerkosten entstehen durch die Kapitalbindungskosten. Das sind Opportunitätskosten für das Kapital, das für die Beschaffung der Lagerbestände eingesetzt wird und nicht anderweitig gewinnbringend verwendet werden kann. Ermitteln kannst du sie, indem du den mittleren Bestand 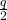$\frac{q}{2}$ mit dem $Lagerkostensatz\ c\ =\ \frac{Lagerkosten}{Durchschnittlicher\ Lagerwert}\ \cdot\ 100$ multiplizierst. Die bestellfixen Kosten entstehen durch Transport- und Personalkosten. Wie du ja bereits weißt, kannst du t dabei auch als $t=\frac{q}{d}$ schreiben.
Betrachten wir die Kosten grafisch, sieht das so aus:

Optimale Losgröße — Kostenfunktion

Die Lagerkosten werden mit zunehmender Bestellmenge immer größer, da mehr Waren gelagert werden müssen. Die Bestellkosten nehmen dagegen mit zunehmender Bestellmenge ab, da nicht so oft bestellt werden muss. Die Kosten verlaufen also gegenläufig. Im Minimum der Gesamtkosten sind die Lager- und die Bestellkosten gleich.
Wir haben also zwei Möglichkeiten die optimale Losgröße zu finden. Zum einen können wir die Lagerkosten mit den bestellfixen Kosten gleichsetzen:

$\frac{c}{2}\ \ast\ q=\frac{F\ *\ d}{q}$

Zum anderen können wir auch die Kostenfunktion nach q ableiten und erhalten so die Formel für unsere optimale Losgröße:

${K'}_{\left(q\right)}=\frac{c}{2}-\frac{F\ *\ d}{q^2}=0$

$q^\ast=\sqrt{\frac{2\ast F\ast d}{c}}$

Um die optimale Bestellmenge berechnen zu können, benötigen wir also die Fixkosten F, die Bedarfsrate d und den Lagerkostensatz c. Im Folgenden nehmen wir an, dass unsere bestellfixen Kosten 300 € betragen. Zudem benötigen wir 500 Bänder pro Woche, was unserer Bedarfsrate entspricht.

Lagerkostensatz der optimalen Bestellmenge

Jetzt müssen wir noch den Lagerkostensatz c berechnen. Für diese Formel benötigen wir den Kapitalbindungssatz i und den Preis p pro Armband. Sagen wir, der Kapitalbindungssatz ist 8% pro Jahr und ein Band kostet 50 €. Da wir in Wochen rechnen, müssen wir unbedingt den Kapitalbindungssatz pro Woche ermitteln. Das sieht dann so aus:

Optimale Losgröße — Lagerkostensatz berechnen

Unser Lagerkostensatz beträgt somit 0,0769 Euro pro Stück und Woche. Das bedeutet, dass dich jedes Armband, dass du auf Lager hast pro Woche 7,69 Cent kostet. Jetzt haben wir alle Werte, die wir brauchen.

Optimale Losgröße berechnen bei Fremdbeschaffung: Optimale Bestellmenge – Andler Formel

Setzen wir die berechneten Werte in die Andler Formel ein, können wir unsere optimale Bestellmenge berechnen:

$q^\ast=\sqrt{\frac{2\ *\ 300\ *\ 500}{0,0769}}=\ 1.975$

Du solltest also 1975 Uhrenbänder auf einmal bestellen.

Optimaler Bestellzyklus für die Optimale Bestellmenge

Jetzt ist die Frage, in welchen Zeitabständen diese Menge geordert werden soll. Um den optimalen Bestellzyklus herauszufinden, musst du die optimale Bestellmenge durch die Bedarfsrate teilen:

Optimale Losgröße — Optimaler Bestellzyklus

Du solltest also alle 3,95 Wochen 1975 Uhrenbänder bestellen.

Minimale Kosten für die Optimale Bestellmenge

Wenn du jetzt noch wissen möchtest wie hoch die Kosten sind, die dir im Minimum wöchentlich entstehen, setzt du einfach die optimale Bestellmenge in die Kostenfunktion ein:

$K_{\left(q\right)}=\frac{q}{2}\ \ast\ c+\frac{F}{t}=\frac{1975}{2}\ \ast\ 0,0769+\frac{300}{3,95}=151,89 \frac{Euro}{Woche}$

Damit kommen wir auf 151, 89 Euro pro Woche.
Möchtest du die minimalen Kosten berechnen, ohne die optimale Bestellmenge zu kennen, kannst du diese Formel verwenden:

$K_{\left(q\right)}^\ast=\sqrt{2\ *\ F\ *\ d\ *\ c}$
$K_{\left(q\right)}=\frac{q}{2}\ \ast\ c+\frac{F}{t}=\frac{1975}{2}\ \ast\ 0,0769+\frac{300}{3,95}=151,89 \frac{Euro}{Woche}$

Setzen wir unsere Werte in diese ein, kommen wir auch so auf 151,89 Euro pro Woche.

Optimale Losgröße bei Eigenproduktion

Bei der Eigenproduktion stellst du die Armbänder selbst her. In der Supply Chain befinden wir uns hier in der Phase der Produktion. Wie du die optimale Losgröße bei Eigenproduktion mit der Andler Formel berechnen kannst, zeigen wir dir hier!

Losgrößenmodell bei Eigenproduktion

Im Vergleich zum Fall der Fremdbeschaffung erweitert sich hier unser Modell um die Variable x. Diese ist die Produktionsgeschwindigkeit, mit der das Los in das Lager kommt. Dabei kommt es nicht wie bei der Bestellung zeitpunktgeballt in das Lager, sondern nach und nach. Um die optimale Losgröße und die optimalen Produktionsabstände herauszufinden, schauen wir uns vorerst wieder eine Grafik dazu an:

Optimale Losgröße — Losgrößenmodell bei Eigenproduktion

Kostenfunktion für die Optimale Losgröße

Schauen wir uns nun an, wie sich die Kostenfunktion zusammensetzt. Sie besteht zum einen, wie bei der Fremdbeschaffung, aus den Lagerkosten, also den Kapitalbindungskosten, und zum anderen aus den losfixen Kosten. Die Kapitalbindungskosten sind hier nun geringer, da der Bestand ja nicht auf einmal, sondern mit der Produktionsgeschwindigkeit zunimmt. Das wird in der Formel berücksichtigt.
Sie erweitert sich um die Komponente $1-\frac{d}{x}$ .

Unter losfixen Kosten versteht man die Rüstkosten. Das sind die Kosten, die dadurch entstehen, dass wir die Maschine auf die Produktion von Uhrenbändern vorbereiten müssen. Das können Personalkosten, Opportunitätskosten für entgangene Deckungsbeiträge oder Materialverlust sein. Um die losfixen Kosten herauszufinden, teilen wir auch hier unsere Fixkosten F einfach durch die Bestellzykluslänge t.

$K_{\left(q\right)}=\frac{q}{2}\ast\left(1-\frac{d}{x}\right)\ast\ c+\frac{F}{t}=\frac{q}{2}\ast\left(1-\frac{d}{x}\right)\ast\ c+\frac{F\ *\ d}{q}$

Grafisch sieht das genauso aus wie bei Fremdbeschaffung der Uhrenbänder.

Optimale Losgröße bei Eigenproduktion – Andler Formel

Leiten wir unsere neue Kostenfunktion nach der Produktionsmenge q ab, erhalten wir die Andler Formel:

$q^\ast=\sqrt{\frac{2\ast F\ast d}{c\ast(1-\frac{d}{x})}}$

Im Folgenden nehmen wir an, dass dir pro Rüstvorgang Kosten in Höhe von 500€ entstehen. Die Bedarfsrate beträgt 500 Bänder pro Woche und die Produktionsgeschwindigkeit 30 Stück pro Stunde. Beachte aber, dass du die Produktionsgeschwindigkeit noch in Wochen umrechnen musst. Hat eine Woche 80 Arbeitsstunden beträgt unsere Produktionsgeschwindigkeit also 2400 Stück pro Woche:

Optimale Losgröße — Andler Formel und Umrechnung der Geschwindigkeit

Lagerkostensatz für die Optimale Losgröße

Jetzt müssen wir nur noch den Lagerkostensatz berechnen. Gehen wir davon aus, die Herstellung eines Uhrenbandes kostet uns 30 €. Der Kapitalbindungssatz sei wieder 8% pro Jahr. Dann ergeben sich 0,0462 Euro pro Stück pro Woche:

Optimale Losgröße — Lagerkostensatz berechnen

Optimale Losgröße berechnen bei Eigenpoduktion – Andler Formel

Jetzt können wir alle Werte ganz einfach in die Andler Formel einsetzen und erhalten unsere optimale Losgröße:

$q^\ast=\sqrt{\frac{2\ast500\ast500}{0,0462\ast(1-\frac{500}{2400})}}=3697$

Du solltest also 3697 Uhrenbänder in einem Los produzieren.

Optimale Zeitabstände für die Optimale Losgröße

Aber in welchen Zeitabständen soll produziert werden? Um das herauszufinden, teilen wir einfach wie vorhin unser optimales Produktionslos durch die Bedarfsrate:

Optimale Losgröße — Optimale Zeitabstände

Die Kosten sind also minimal, wenn du alle 7,4 Wochen 3697 Uhrenbänder produzierst.

Kosten berechnen für die Optimale Losgröße

Wenn wir jetzt noch die wöchentlichen Kosten berechnen wollen, wenn wir die optimale Losgröße produzieren, setzen wir diese wie vorhin einfach in unsere Kostenfunktion ein:

$K_{\left(q\right)}=\frac{q}{2}\ast\left(1-\frac{d}{x}\right)\astc+\frac{F\ \ast\ d}{q}=\frac{3697}{2}\ast\left(1-\frac{500}{2400}\right)\ast\ 0,0462+\frac{500\ \ast\ 500}{3697}$
$=135,23\frac{Euro}{Woche}$

Es entstehen dir also Kosten von 135,23 € pro Woche bei Eigenherstellung der Uhrenbänder.

Jetzt weißt du, wie du die optimale Losgröße und die optimale Bestellmenge mit der Andler Formel ermitteln kannst.

Beliebte Inhalte aus dem Bereich Produktion & Logistik

Intro Produktion und Logistik II

Losgrößenmodell bei Fremdbeschaffung

Losgrößenmodell bei Eigenproduktion

Ablaufplanung - Prioritätsregeln

Ablaufplanung - Moore- und Johnson-Algorithmus

Ablaufplanung - Job-Shop

Tourenplanung - Savings-Verfahren

Tourenplanung - Sweep-Verfahren

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .