Reelle Zahlen – Exzeß-q und Festkomma
Du möchtest wissen, was das Exzess-q und die Festkommazahl sind? Im Folgenden erklären wir dir die beiden Begriffe und wie die Umwandlungen funktionieren.
Inhaltsübersicht
Exzessdarstellung, Bias und Festkommazahl
Beginnen wir mit der Exzess-q-Darstellung. Am Anfang steht immer die Frage des Warum. Wozu brauchen wir diese Form der Darstellung überhaupt und was kann sie? Wir können mit einem Rechner immer eine bestimmte Anzahl an Zahlen angeben, deren Menge von der Länge der benutzen Bitfolge abhängt. Standardmäßig starten diese Zahlen immer bei null. Das heißt für uns: Negative Zahlen gibt es keine und auch nach oben sind unsere Möglichkeiten beschränkt.
Aber genau das ist es, was die Exzess-q-Codierung ändert. Sie ermöglicht es uns, unseren unteren Grenzwert beliebig zu verschieben. Das bedeutet, dass wir weniger Freiheit nach oben, dafür aber negative Zahlen haben, wenn wir ihn nach unten verschieben. Andererseits verlieren wir, indem wir ihn nach oben verschieben, die Möglichkeit kleinere Zahlen darzustellen, können dafür aber mehr höherwertige hinzugewinnen.
Bias berechnen
Diesen Grenzwert nennt man auch Bias. Oft ist er vorgegeben. Er muss manchmal aber auch errechnet werden. Das geht mit der Formel:

Dabei ist l die Länge in Bit und bezieht sich damit auf die Binärdarstellung der Zahl. Nehmen wir einmal an, wir wollen die Binärzahl 1001 in Exzess-q-Schreibweise darstellen.
Dann müssen wir jetzt zuerst den Bias errechnen. Dazu setzen wir „vier“ in unsere Formel ein. Zwei hoch drei sind acht und acht minus eins sind sieben. Unser Bias ist also sieben. Die allgemeine Schreibweise für Exzess-q lautet:

Hier steht das EX ganz einfach für die Art der Codierung, also Exzess. Das q symbolisiert den Bias und das n die Länge der binären Schreibweise. X ist die Zahl, die wir codiert haben. In unserem Fall ist X neun, da

Nun können wir alle Werte einsetzen und erhalten:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Festkomma-Arithmetik– allgemeine Schreibweise
Es gibt aber nicht nur ganze Zahlen, sondern auch Dezimalbrüche. Diese zu codieren ist etwas komplizierter. Es gibt zwei verschiedene Arten, dies zu tun. Zum einen die Gleitkommazahl und zum anderen die Festkommazahl, die wir hier genauer betrachten. Genauso wie die Exzess-q-Darstellung hat auch die Festkommacodierung eine allgemeine Schreibweise:
Dabei steht FK für Fest-Komma und auch n behält seine vorgesehene Bedeutung. Einzig neu ist das k, das unser q ersetzt hat. Es ist aber bei genauerem Hinschauen nicht gerade ein Rätsel, wofür es steht. Schließlich ist das einzig andere, dass wir jetzt Nachkommastellen haben. Dementsprechend steht das k also für die Anzahl unserer Nachkommastellen. Daraus können wir aber noch eine weitere Information gewinnen. Denn wenn n unsere Gesamtanzahl an Stellen ist und k unsere Nachkommastellen, dann ist n-k die Menge unserer Vorkommastellen.
Absolute und relative Rundungsfehler
Zwar können wir nun Nachkommastellen darstellen, allerdings kann unser Rechner nicht richtig runden oder zumindest tut er es nicht ohne, dass wir eine gesonderte Funktion dafür benutzen. Wenn wir diese Funktion verwenden, sind unsere Werte nur exakt, wenn die Anzahl der Nachkommastellen kleiner k ist. Wenn das nicht zutrifft, können Rundungsfehler entstehen.
Wir unterscheiden dabei zwischen zwei verschiedenen Auswertungen: Dem absoluten und dem relativen Rundungsfehler. Der absolute Rundungsfehler wird berechnet, indem wir die korrekte Zahl von der falsch gerundeten Zahl subtrahieren und davon den Betrag bilden. Der relative Rundungsfehler wird ähnlich gebildet. Wir erweitern lediglich die Formel, indem wir unserem absoluten Rundungsfehler durch den Betrag von X alt teilen.
Reelle Zahlen – Übung zu Exzess-q und Festkomma
Nun wollen wir uns die beiden Kodierungen noch an einem kurzen Beispiel anschauen.
Umwandlung Binärzahl in Exzess-q
Beim ersten Beispiel haben wir eine Binärzahl gegeben und wollen sie in die Exzess-q-Darstellung umwandeln. Nehmen wir doch einfach einmal die 1010. Jetzt müssen wir als erstes den Bias errechnen. Dafür benötigen wir die wieder die Formel:  .
.
Für l setzen wir jetzt die Länge unserer Binärdarstellung ein. Also ist  . Damit erhalten wir sieben. Als nächstes können wir die allgemeine Schreibweise verwenden. Für q können wir schonmal unseren Bias einsetzen. Auch n können wir festlegen, denn dabei handelt es sich um die originale Länge unserer Binärzahl. Die Zahl X zu erhalten ist ebenfalls kein Hexenwerk, denn x ist die Dezimaldarstellung unserer Binärzahl. Dafür übersetzen wir also
. Damit erhalten wir sieben. Als nächstes können wir die allgemeine Schreibweise verwenden. Für q können wir schonmal unseren Bias einsetzen. Auch n können wir festlegen, denn dabei handelt es sich um die originale Länge unserer Binärzahl. Die Zahl X zu erhalten ist ebenfalls kein Hexenwerk, denn x ist die Dezimaldarstellung unserer Binärzahl. Dafür übersetzen wir also  in ihre Dezimaldarstellung.
in ihre Dezimaldarstellung.
Dazu gehen wir die Ziffern von rechts nach links durch und multiplizieren sie mit der entsprechenden Potenz von zwei. Das heißt, wir rechnen:
Wenn wir das alles am Ende zusammenrechnen, dann erhalten wir als Ergebnis die Binärzahl zehn. Jetzt müssen wir sie nur noch für x einsetzen und haben eine vollständige Exzess-q-Darstellung.
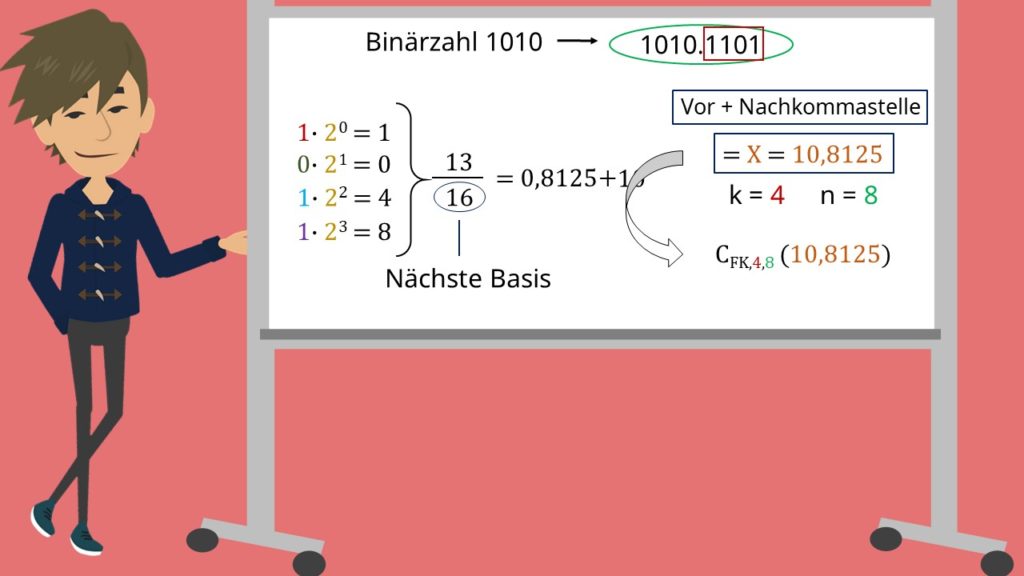
Beispiel Festkommazahl
Als Binärzahl nehmen wir uns einfach nochmal unsere 1010, aber ergänzen sie durch Nachkommastellen:  . Nun können wir bereits k und n in die allgemeine Formel einsetzen, indem wir für n die gesamten Stellen unserer Binärzahl zählen und für k die Anzahl der Nachkommastellen. Das heißt n ist acht und k ist gleich vier. Damit fehlt uns also noch das x.
. Nun können wir bereits k und n in die allgemeine Formel einsetzen, indem wir für n die gesamten Stellen unserer Binärzahl zählen und für k die Anzahl der Nachkommastellen. Das heißt n ist acht und k ist gleich vier. Damit fehlt uns also noch das x.
Dafür müssen wir – genau wie bei der Exzess-q-Darstellung – unsere Binärzahl in eine Dezimalzahl umwandeln. Praktischerweise haben wir das für die Vorkommastellen schon erledigt, sodass wir uns nur noch um die Nachkommastellen kümmern müssen. Dazu arbeiten wir die Ziffern nach dem Komma von rechts nach links durch und multiplizieren sie mit der entsprechenden Potenz von zwei. Wir rechnen also:
Damit erhalten wir als Ergebnis dreizehn. Da es sich hier aber um Nachkommastellen handelt, müssen wir diese Zahl jetzt noch durch die Basis, die als nächstes kommen würde, also durch die sechzehn teilen. Wenn wir jetzt Vorkomma- und Nachkommastellen zusammenführen, ist unser x gleich 10,8125. Jetzt setzen wir alles in die allgemeine Formel ein und erhalten unser Endergebnis.
Jetzt weißt du nicht nur, wie du Zahlen problemlos umwandelst, sondern kannst dieses Wissen auch konkret anwenden.