Kirchhoffsche Regeln
In diesem Artikel erklären wir dir die Kirchhoffschen Regeln. Wir gehen also genauer auf die Knoten- und Maschenregel ein und demonstrieren dir ihre Anwendung anhand eines Beispiels.
Schau auch gerne in unser Video rein. Darin begleiten wir dich Schritt für Schritt durch das Thema.
Inhaltsübersicht
Kirchhoffsche Regeln einfach erklärt
Die Kirchhoffschen Regeln kannst du dir als Grundlage einer jeden Schaltungsanalyse vorstellen. Auf dieser Grundlage bauen weitere fortgeschrittene Methoden auf. Bei den Kirchhoffschen Regeln handelt es sich um zwei Grundsätze:
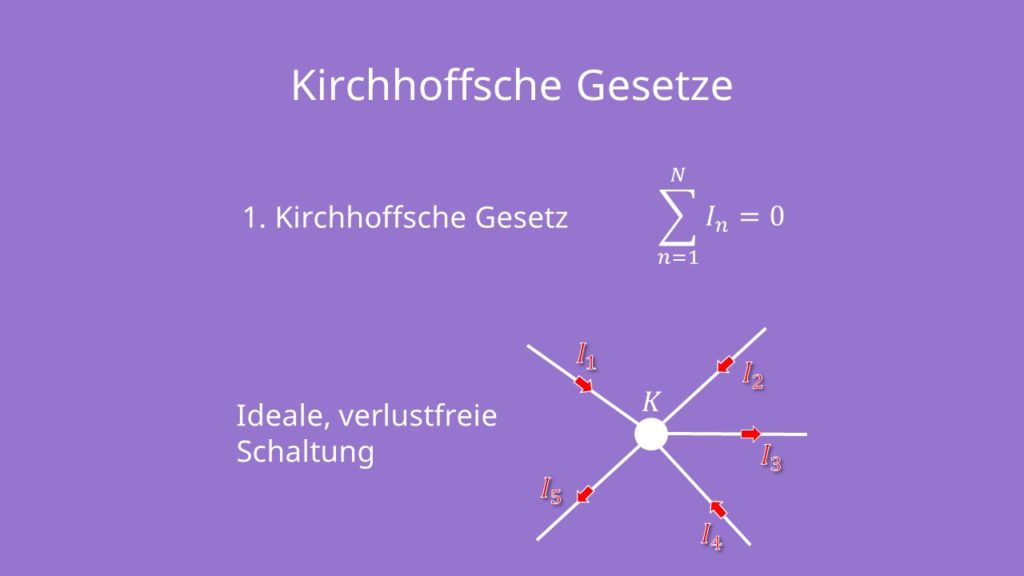
Die erste Kirchhoffsche Regel, auch Knotenregel oder Knotensatz genannt besagt, dass die Summe aller Ströme an einem Knoten gleich Null sein muss.
Die zweite Kirchhoffsche Regel wird auch als Maschenregel oder Maschensatz bezeichnet. Laut ihr ist die Summe der Spannungen in einer Masche gleich Null.
Erste Kirchhoffsche Regel: Knotenregel
Die erste Kirchhoffsche Regel, wird als Knotenregel oder Knotensatz bezeichnet. Sie besagt, dass die Summe aller Ströme an einem Knoten gleich Null ist. Das bedeutet: Die Summe der in einen Knotenpunkt zufließenden Ströme ist gleich der Summe der abfließenden Ströme. Wäre dem nicht so, dann wäre in dem Knoten ein wachsender Ladungshaufen, was physikalisch nicht möglich ist. Dabei gehen wir hier von einer idealen, verlustfreien Schaltungen aus. In unserem Beispiel haben wir einen beliebigen Knoten „K“ und fünf Ströme. Die Richtung der bereits eingezeichneten Stromzählpfeile nehmen wir vorerst so an:
Im folgenden Kapitel stellen wir die Gleichung für die Ströme im Knotenpunkt auf.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Vorzeichenregeln der Ströme
Um die zugehörige Kirchhoffsche Gleichung aufzustellen, benötigst du eine Regel zur Festlegung des Vorzeichens der einzelnen Ströme:
- Fließt der Strom in den Knoten hinein, dann ist er positiv.
- Fließt der Strom aus dem Knoten hinaus, dann ist sein Vorzeichen negativ.
Für unser Beispiel mit dem Knoten K gilt also die folgende Gleichung:

An dieser Stelle ist es wichtig anzumerken, dass die tatsächliche Stromrichtung beim Aufstellen der Gleichung unwichtig und meistens auch gar nicht bekannt ist. Es wird nur die Richtung berücksichtigt, die mittels Stromzählpfeil eingezeichnet und somit angenommen wurde. Falls die eingezeichnete Richtung in der Realität nicht zutreffen sollte, dann ergibt sich bei der Berechnung ein negativer Strom.
Beispiel der Knotenregel
Die Anwendung der Knotenregel demonstrieren wir dir am folgenden Beispiel:
Gesucht sind hier die Knotengleichungen für die eingezeichneten Knotenpunkte  ,
,  und
und  . Zudem suchen wir die Maschengleichungen für die Maschen
. Zudem suchen wir die Maschengleichungen für die Maschen  ,
,  und
und  . Die Richtung der einzelnen Strom- und Spannungspfeile sind nicht vorgegeben und können daher frei gewählt werden.
. Die Richtung der einzelnen Strom- und Spannungspfeile sind nicht vorgegeben und können daher frei gewählt werden.
Wir beginnen mit dem Aufstellen der Knotengleichungen und gehen folgendermaßen vor:
Zuerst zeichnest du die Ströme ein, deren Richtung frei wählbar ist. Der Spannungspfeil der Spannungsquelle ist mit  bereits vorgegeben. Folglich geht der aus
bereits vorgegeben. Folglich geht der aus  herausfließende Gesamtstrom
herausfließende Gesamtstrom  nach oben. Die Indizes der einzelnen Ströme kannst du nach den Indizes der Widerstände wählen. Der Gesamtstrom fließt über den Widerstand
nach oben. Die Indizes der einzelnen Ströme kannst du nach den Indizes der Widerstände wählen. Der Gesamtstrom fließt über den Widerstand  und heißt somit
und heißt somit  .
.
Nach dem Einzeichnen der Ströme, sieht die Schaltung folgendermaßen aus:
Da zwischen den Widerständen  und
und  keine Abzweigung existiert, gilt:
keine Abzweigung existiert, gilt:
 .
.
Den Strom  kann man somit auch wegstreichen und durch
kann man somit auch wegstreichen und durch  ersetzen.
ersetzen.
Jetzt kannst du die Gleichungen für die einzelnen Knoten aufstellen.



Die zweite Kirchhoffsche Regel: Maschenregel
Bei der zweiten kirchhoffschen Regel, auch Maschenregel oder Maschensatz genannt, werden die Spannungen betrachtet. Die Summe aller Spannungen in einer Masche ist Null. Dahinter steckt der Energie-Erhaltungssatz: In einen geschlossenen Umlauf muss genau so viel Energie hineingesteckt werden, wie auch wieder herausgeholt wird. Das entspricht dem idealen, verlustfreien Fall, von dem wir hier ausgehen.
Vorzeichenregeln der Spannungen
Schauen wir uns ein Beispiel mit der Masche  an. Sie umfasst eine Spannungsquelle mit der Spannung
an. Sie umfasst eine Spannungsquelle mit der Spannung  und vier Widerständen sowie den über ihnen abfallenden Spannungen
und vier Widerständen sowie den über ihnen abfallenden Spannungen  . Auch hier müssen wir die Richtungen der Spannungspfeile berücksichtigen.
. Auch hier müssen wir die Richtungen der Spannungspfeile berücksichtigen.
Das Vorzeichen der Spannung richtet sich nach folgender Definition:
- Zeigen der Spannungspfeil und der Maschenpfeil in die gleiche Richtung, dann ist das Vorzeichen der Spannung positiv.
- Zeigt die Richtung der Spannung entgegengesetzt zum Maschenumlauf, dann ist das Vorzeichen negativ.
Für unser Beispiel gilt also:

Auch hier ist die Richtung der einzelnen Spannungen reine Definitionssache. Üblich ist es aber, dass Strom und Spannung in die gleiche Richtung zeigen.
Beispiel der Maschenregel
Zuerst zeichnen wir hier die Spannungspfeile ein. Dabei orientieren wir uns an den bereits eingezeichneten Strömen, denn die Spannungen zeigen üblicherweise in die gleiche Richtung wie die definierten Ströme. Die Indizes wählen wir auch entsprechend den Widerständen.
Um uns einen besseren Überblick über die Masche  zu verschaffen blenden wir die Teile der Schaltung die nicht zu Masche
zu verschaffen blenden wir die Teile der Schaltung die nicht zu Masche  gehören aus.
gehören aus.
Wir ignorieren also  und
und  . Unsere Masche sieht dann so aus:
. Unsere Masche sieht dann so aus:
Die Maschengleichung ergibt sich aus der Richtung eines Maschenumlaufs (hier gelb eingezeichnet). Basierend auf der Maschenregel wissen wir bereits, dass die Summe aller Spannungen Null sein muss. Alle Spannungen die in die gleiche Richtung zeigen, werden positiv und entgegen gerichtete Spannungen negativ berücksichtigt. Für Masche  ergibt sich damit:
ergibt sich damit:

Für die anderen Maschen gehen wir genauso vor. Wir betrachten dabei jeweils nur den Teil der Schaltung den die Masche umfasst. Daraus ergibt sich: