Video

Funktionenfolgen: Punktweise Konvergenz

Die punktweise Konvergenz von Funktionenfolgen bereitet dir noch Schwierigkeiten? Im Folgenden zeigen wir dir Schritt für Schritt die Vorgehensweise bei der punktweisen Konvergenz.

Inhaltsübersicht

Konvergenz von Funktionenfolgen: Definition Funktionenfolge und punktweise konvergent

Wenn die Glieder f_n einer Folge von einem Parameter abhängen, spricht man von einer Funktionenfolge. $f_n(x)=\frac{x}{n}$ ist beispielsweise eine Funktion von und gleichzeitig eine Folge. Die einzelnen Folgenglieder erhält man, indem man für eine beliebige natürliche Zahl einsetzt, zum Beispiel $f_2\left(x\right)=\frac{x}{2}$ oder $f_3\left(x\right)=\frac{x}{3}$ .

Definition punktweise Konvergenz

Existiert für jedes $x\in\ I$ der Grenzwert:

$f\left(x\right)=\(\lim\limits_{n \to \infty} \ f_n\left(x\reight)$

dann ist die Funktionenfolge punktweise konvergent und 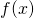f(x) heißt Grenzfunktion der Funktionenfolge.

Punktweise Konvergenz Beispiel

Dann schauen wir uns jetzt mal ein Beispiel zur punktweisen Konvergenz an und zwar die Funktionenfolge x^n .

Punktweise Konvergenz Beispiel

Wird $x\in\left[0;\ 0,9\right]$ auf der Menge der reellen Zahlen abgebildet, ergibt sich die Grenzfunktion zu

$f\left(x\right)=\(\lim\limits_{n\rightarrow\infty\ }{f_n\left(x\right)}=\(\lim\limits_{n\rightarrow\infty\ }x^n=0$

denn eine geometrische Folge, deren Basis im Betrag kleiner als 1 ist, ist eine Nullfolge.

Ändern wir nun den Definitionsbereich von auf $\left[0,\ 1\right]$ , bleibt die Grenzfunktion für alle x-Werte echt kleiner 1 dieselbe, nämlich Null. Für x=1 jedoch ist der Grenzwert . Die Grenzfunktion ist in diesem Fall nicht stetig, obwohl alle Folgenglieder x^n stetig sind.

Für $x\in\left[-1;\ 1\right]$ gilt im Punkt x=-1 :

$f\left(x\right)=\(\lim\limits_{n\rightarrow\infty\ }{(-1)}^n$

Die Folge ${(-1)}^n$ hat keinen Grenzwert. Das bedeutet, dass die Funktionenfolge auf dem Intervall $x\in\left[-1;\ 1\right]$ nicht punktweise konvergent ist.

Gehen wir nun zurück zum Intervall $\left[0;1\right]$ . An diesem Beispiel kann man sehen, dass sich Folgen- und Funktionsgrenzwert im Allgemeinen nicht vertauschen lassen.

Punktweise Konvergenz Beispiel

Bilden wir zunächst die Grenzfunktion 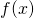f(x) , indem wir gegen Unendlich laufen lassen und lassen danach gegen gehen, ergibt sich Null. Umgekehrt, also wenn wir erst den Grenzwert für gegen bilden, also praktisch f_n(1) auswerten und anschließend den Limes für gegen Unendlich bestimmen, ergibt sich der Grenzwert .

Genauso wenig lassen sich Integration und Folgengrenzwert vertauschen oder Differentiation und Folgengrenzwert. Allerdings sind derartige Vertauschungen möglich, wenn die Konvergenz der Funktionenfolge strengeren Bedingungen genügt.

Wir konnten hoffentlich all deiner Verwirrung zum Thema Funktionenfolgen ein Ende setzen und Licht ins Dunkel bringen, wenn es zu punktweiser Konvergenz von Funktionenfolgen kommt.

Beliebte Inhalte aus dem Bereich Mathe für Ingenieure

Intro Funktionenreihen

Funktionenfolgen - punktweise Konvergenz

Funktionenfolgen - gleichmäßige Konvergenz

Funktionenreihen

Taylorreihen - Landausymbol

Taylorreihen - Anwendung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .