Feuchte Luft – Zustandsgrößen
Wie du weißt, ist nach dem Duschen das Badezimmer immer deutlich wärmer. Um das zu beschreiben, benötigen wir die Zustandsgrößen der feuchten Luft, die wir uns jetzt genauer anschauen.
Inhaltsübersicht
Zustandsgrößen
Du hast bereits gelernt wie man die absolute und relative Luftfeuchtigkeit berechnet. Nun wollen wir uns jetzt noch den Zustandsgrößen zuwenden. Diese ändern sich für feuchte Luft, je nachdem wie viel Wasser in der Luft ist. Wir betrachten zunächst das Volumen. Das können wir ausdrücken mit:

Der Index L steht dabei für Luft und der Index W für Wasser. Bei feuchter Luft wollen wir immer alles in Bezug auf die trockene Luft betrachten. Diese dient als Referenz, da wir bei Temperaturen immer eine relative Betrachtung machen.
Volumen
Also teilen wir durch „m L“ und erhalten das spezifische Volumen der feuchten Luft:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beladung
Den Quotienten wollen wir zur Vereinfachung mit der Beladung X ausdrücken. Somit ergibt sich:

Enthalpie
Analog können wir auch für die Enthalpie vorgehen.

Diese lässt sich ebenfalls über die Beladung ausdrücken:

Die Enthalpie der Luft bekommen wir über die kalorische Zustandsgleichung:

Die Enthalpie des Wassers setzt sich zum einen aus der Verdampfungsenthalpie und zum anderen aus der Enthalpie-Änderung durch eine Temperaturerhöhung zusammen.

Da wir uns ja immer auf die trockene Luft beziehen, sind sowohl die Verdampfungsenthalpie, als auch die Temperaturdifferenz auf diese bezogen.
Entropie
Für die Entropie ergibt sich das ähnlich:


Allerdings wissen wir aus den Zustandsgleichungen, dass die Entropie druckabhängig ist. Zudem ist hier natürlich auch eine Verdampfungsentropie Delta s v miteinzubeziehen. Das heißt für die Entropie der trockenen Luft erhalten wir:

Und für die des Wasserdampfs:

Beispiel
Klingt alles noch etwas komplex. Deshalb betrachten wir jetzt einen Raum mit der Beladung X gleich 0,012. Dieser hat eine Temperatur von 273,16 Kelvin. Der Druck von Luft entspricht ein Bar. Der Partialdruck des Wassers ist 1,9 Kilopascal. Die Molare Masse von Luft ist 28,964 Gramm pro Mol und die von Waser 18,015 Gramm pro Mol. Die ideale Gaskonstante kennen wir als 8,314 Joule pro Mol Kelvin.
Damit wollen wir jetzt die Enthalpie und die Entropie der feuchten Luft im Raum berechnen. Wir beginnen mit der Enthalpie:

Die Enthalpie der Luft ist Null, da wir uns genau bei der Referenztemperatur von 273,16 Kelvin befinden:

Für die Enthalpie des Wassers müssen wir nur die Verdampfungsenthalpie betrachten. Aus der Literatur wissen wir, dass diese 2500 Kilojoule pro Kilogramm ist.

Damit erhalten wir für die Enthalpie der feuchten Luft:

Das heißt die Enthalpie der feuchten Luft ist um 30 Kilojoule pro Kilogramm größer als die der trockenen Luft.
Als nächstes kümmern wir uns um die Entropie. Wir betrachten wieder die Entropie der Luft und des Wassers einzeln. Hier können wir die Terme der Temperatur streichen, da gilt:

Wir beginnen wieder mit der trockenen Luft. Dafür benötigen wir deren Druck. Diesen erhalten wir aus dem Gesamtdruck und dem Druck von Wasser, da der Gesamtdruck die Summe aller Partialdrücke ist:

Setzen wir nun alle Werte ein, ergibt sich:

Als nächstes bestimmen wir die Entropie des Wassers. Die Verdampfungsentropie erhalten wir wieder aus der Literatur mit 9,1562 Kilojoule pro Kilogramm Kelvin. Damit können wir uns die Entropie des Wassers bestimmen zu:

Damit erhalten wir für die Entropie der feuchten Luft:
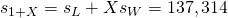
Durch das Vorzeichen können wir erkennen, dass sich die Entropie der Luft erhöht. Die feuchte Luft sorgt somit für eine Enthalpie- und Entropiesteigerung.
Du siehst: Dass das Badezimmer nach dem Duschen wärmer ist, hängt nicht nur mit der Erwärmung des Raumes zusammen, sondern auch damit, dass das Wasser die Enthalpie der Luft erhöht. Bis bald!


