Video

Auflagerkräfte berechnen

In diesem Beitrag wollen wir dir erklären, wie man Lagerkräfte bzw. Auflagerkräfte berechnen kann. Außerdem zeigen wir dir alles, was du zu Lagerreaktionen bzw. Auflagerreaktionen wissen musst. Falls du dabei noch nicht ganz sicher bist, ob du die Theorie komplett verstanden hast, schau dir doch nochmal unseren Beitrag zu dem Festlager und Loslager an!

Inhaltsübersicht

Auflagerkräfte und Lagerreaktionen ermitteln

Zu Beginn klären wir noch einmal die Grundlagen: Es gibt verschiedene Arten von Lagerungen und je nach Lager haben wir unterschiedliche Lagerreaktionen. Grundsätzlich können Kräfte und Momente aufgenommen werden. Das heißt, dass die jeweilige Lagerung eine Art Widerstand gegen die von außen einwirkende Belastung bildet, die sogenannte Lagerreaktion. Ziel ist es nun heraus zu finden, welche Belastung jedes einzelne Lager erfährt.

Die einzelnen Lagerarten und ihre grafische Darstellungen findest du in folgendem Bild.

Auflagerkräfte, Loslagerkräfte, Feste Einspannung, Momentengelenk, Loslager, Festlager, Lagerarten, Statik — Lagerarten Mechanik

Auflagerreaktionen berechnen

Wir betrachten jetzt einen einfachen Balken, der durch ein Festlager auf der linken Seite und durch ein Loslager auf der rechten Seite befestigt ist. Zur besseren Orientierung nennen wir das Festlager „Lager A“ und das Loslager „Lager B“. Der Balken hat die Länge gleich und wird durch eine quadratische Linienlast mit einem q_0 von $30 \frac{N}{m}$ Newton pro Meter belastet. Die Last wird beschrieben durch:

$q\left(x\right)=q_0\times\frac{x^2}{L^2}$

Nachdem wir unser System jetzt kennen, müssen wir im ersten Schritt prüfen, ob es auch statisch bestimmt ist. Die Theorie hierzu haben wir dir hier verlinkt. Da wir hier einen ebenen Balken betrachten, ergibt sich die Formel für das Aufzählungskriterium:

$f=3k-\left(a+z\right)$

Auflagerkräfte, Lagerreaktionen, Auflagerreaktionen, Festlager, Loslager, Abstand, statische Bestimmtheit — Auflagerreaktionen berechnen

Lagerkräfte und Lagerreaktionen

Bevor wir jetzt die Lagerkräfte berechnen, müssen wir zunächst die Lagerreaktionen und die Auflagerkräfte bestimmen. Da wir hier nur einen Balken haben, ist k = 1 . Das ist auch der Grund, warum keine Zwischenreaktionen stattfinden können und z = 0 ist. Nun müssen wir nur noch die Auflagerkräfte zählen: Wie du sicher noch weißt, hat ein Festlager zwei Lagerreaktionen und ein Loslager nur eine Lagerreaktion. 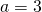Daraus ergibt sich, dass a = 3 ist. Jetzt können wir auch $\mathbf{f}$ bestimmen:

$f=3\times1-\left(3+0\right)=0$

Somit ist das System statisch bestimmt und wir können weiterrechnen. Um Fehler zu vermeiden, ist es in der Regel sinnvoll, wenn du die Zahlen erst am Ende in deine endgültige Formel einsetzt.

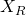Da wir hier eine Linienlast und keine Einzelkraft haben, erschwert das unsere Berechnung ein wenig. Doch wie du dir vielleicht denken kannst, hat auch diese Linienlast eine resultierende Kraft $\mathbf{R}$ und einen Angriffspunkt X_R . Da die Linienlast nur die Ableitung der Querkraft darstellt, können wir einfach bestimmen, indem wir die Linienlast über die Balkenlänge integrieren:

$R=\int_{0}^{L}q\left(x\right)dx=\int_{0}^{L}{q_0\times\frac{x^2}{L^2}dx}=\frac{q_0L}{3}$

Angriffspunkt und Auflagerkräfte berechnen

Auflagerkräfte, Lagerreaktionen, Auflagerreaktionen, resultierende Kraft, Festlager, Loslager, Lagerarten Statik — Auflagerkräfte und Auflagerreaktionen – Angriffspunkt berechnen

Etwas komplizierter ist es, den Angriffspunkt herauszufinden. Doch wenn du dir die Skizze noch einmal anschaust, kannst du dir vielleicht denken, dass die Kraft im Flächenschwerpunkt angreift. Dementsprechend können wir einfach die Formel für den Flächenschwerpunkt anwenden. Allerdings nehmen wir statt einer Fläche die vorher berechnete resultierende Kraft. Im Endeffekt beschreibt diese auch nur den Flächeninhalt des Verlaufes der Linienlast. Da wir aber keine einfache Form haben, auf die wir es reduzieren können, müssen wir die allgemeine Definition verwenden:

$x_R=\frac{1}{R}\int_{0}^{L}{x\times q\left(x\right)dx}=\frac{1}{R}\int_{0}^{L}{q_0\times\frac{x^3}{L^2}dx}=\frac{1}{R}\frac{q_0L^2}{4}=\frac{3}{4}L$

Somit greift unsere Kraft in einem Abstand von $\frac{3}{4} L$ zum Lager an. Super! Einen Großteil hast du damit schon geschafft!

Lagerreaktionen berechnen

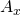Nachdem wir jetzt den Betrag und den Ort der resultierenden Kraft $\mathbf{R}$ herausgefunden haben, kommen wir zur Berechnung der Lagerreaktionen. Schneiden wir den Balken nun frei von den eigentlichen Lagern, erhalten wir die jeweiligen Lagerreaktionen. Das Festlager hat, wie bereits gesagt, zwei Auflagerreaktionen: eine horizontale Auflagerkraft A_x und eine vertikale Auflagerkraft A_y . Das Loslager besitzt nur eine Lagerreaktion: eine vertikale Auflagerkraft B_y . Wir nehmen jetzt an, dass die Vertikalkräfte positiv nach oben zeigen und die Horizontalkraft positiv nach rechts zeigt. Ist die Kraft anders herum anzunehmen, wird das Ergebnis ein negatives Vorzeichen haben.
Um nun die einzelnen Kräfte zu berechnen, verwenden wir einfach die Gleichgewichtsbedingung:

$\sum{H=0=A_x}$
$\sum{V=0=A_y+B_y-R}$
$\sum{M_A=0=B_y\times L-R\times\left(L-x_R\right)}$

Auflagerkräfte, Lagerreaktionen, Auflagerreaktionen, resultierende Kraft, freischneiden, statische Bestimmtheit — Auflagerreaktionen berechnen

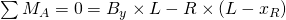
Wir erkennen also, dass die Horizontalkraft 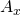A_x gleich Null ist. Aus der Summe der Momente ergibt sich noch:

$B_y=\frac{R\left(L-x_R\right)}{L}=\frac{R\left(L-\frac{3}{4}L\right)}{L}=\frac{R\bullet\frac{1}{4}L}{L}=\frac{\frac{q_0L^2}{12}}{L}=\frac{q_0L}{12}=7,5N$

Das können wir dann in die Gleichung der Vertikalkräfte einsetzen und erhalten:

$A_y=R-B_y=\frac{q_0L}{3}-\frac{q_0L}{12}=\frac{q_0L}{4}=22,5N$

Somit ist die Vertikalkraft A_y = 22,5N .

Beliebte Inhalte aus dem Bereich Mechanik: Statik

Intro Mechanik: Statik I

Lagerreaktionen I

Lagerreaktionen II

Ebene Fachwerke

Schnittverfahren bei Fachwerken

Knotenschnittverfahren

Ritter'scher Schnitt

Schwerpunktberechnung

Schnittgrößen I

Schnittgrößen II

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .