Video

Grenzprodukt und Grenzrate der technischen Substitution

In der Mikroökonomie spielt das Grenzprodukt und die Grenzrate der Substitution eine wichtige Rolle, um den zusätzlichen Ertrag für weitere Inputfaktoren zu ermitteln. In diesem Artikel liefern wir eine Definition, zeigen wie sich das Grenzprodukt berechnen lässt und gehen dann auf die Grenzrate der Substitution genauer ein.

Dich interessiert das Thema – willst aber nicht den kompletten Beitrag durchlesen? Dann schau dir jetzt unser Video zum Grenzprodukt und der Grenzrate der Substitution an!

Inhaltsübersicht

Grenzprodukt Definition

Das Grenzprodukt ist in der mikroökonomischen Produktionstheorie der marginalen Ertragszuwachs durch den zusätzlichen Einsatz eines Produktionsfaktors. In der Regel ist herrscht ein abnehmendes Grenzprodukt vor. Das Grenzprodukt, auf Englisch „Marginal Product“ (MP), gibt an, wie sich der Output des Unternehmens verändert, wenn die Menge einer der beiden Inputfaktoren variiert.

Wir gehen davon aus, dass wir nur zwei Inputfaktoren haben, Zum Beispiel Arbeit und Kapital. In diesem Fall handelt es sich um ein abnehmendes Grenzprodukt. Das siehst Du daran, dass sich der Outputzuwachs immer weniger erhöht je mehr Du bereits von dem Input eingesetzt hast. Der zusätzliche Ertrag für die Faktoren Arbeit und Kapital ist bei steigendem Faktoreinsatz abnehmender Art.

abnehmendes Grenzprodukt, Grenzprodukt Beispiel, — abnehmendes Grenzprodukt

Grenzprodukt der Arbeit

Ein gutes Beispiel für das Grenzprodukt der Arbeit wäre, wenn das x_1 für die Pflücker eines Weinbauern stehen würden. Der erste Pflücker bringt dem Bauern besonders viel Ertrag, da er sich die besten Pflanzen mit den meisten Trauben aussuchen kann. Der zweite Pflücker muss sich dann schon mit den weniger ertragreichen Pflanzen genügen und bringt dem Bauern weniger Ertrag als der erste Pflücker. Der dritte Pflücker erntet noch weniger Trauben usw.. Der Output sinkt also um jede zusätzlich eingesetzte Inputfaktoreinheit.
Die Menge für den anderen Inputfaktor x_2 , z.B. leere Weinflaschen, ist schon festgelegt und lässt sich nicht verändern. In diesen Fall geht es allein um die Auswirkung auf den Output bei der Veränderung von x_1 .

Grenzprodukt der Arbeit, Grenzprodukt des Kapital, — Grenzprodukt der Arbeit

Grenzprodukt berechnen

Im nächsten Schritt zeigen wir Dir, wie Du das Grenzprodukt berechnest. Das ist auch gar nicht so schwer!
Du brauchst zunächst eine Produktionsfunktion. Bei uns lautet sie:

$y\left(x_{1,}x_2\right)={x_1}^{0,25}\ast{x_2}^{0,5}$ .

Dann setzten wir noch die Menge der Weinflaschen auf $\bar{x_2}=100$ fest, da wir ja nur das Grenzprodukt der Arbeit (Pfücker) x_1 berechnen wollen. Jetzt können wir auch schon mit Rechnen anfangen! Setzen wir die 100 für x_2 in unsere Formel ein, bekommen wir die Funktion

$y\left(x_{1,}\ \bar{x_2}\right)=10{x_1}^{0,25}$ .

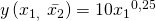Für den Grenzertrag musst Du jetzt nur noch die Produktionsfunktion nach x_1 ableiten. Das sieht dann so aus:

${MP}_1=\frac{\partial y\left(x_{1,}\bar{x_2}\ \right)}{\partial x_1} = 2,5{x_1}^{-0,75}$ .

Wenn du jetzt noch einen Wert für x_1 , z.B. 29 einsetzt, hast du auch schon Dein Grenzprodukt bestimmt. In dem Fall wäre es jetzt bei

${MP}_1=0,2$ .

Grenzprodukt berechnen, Grenzprodukt, Grenzprodukt Formel — Grenzprodukt berechnen

Grenzrate der technischen Substitution Definition

Die Grenzrate der technischen Substitution, auf Englisch „Technical Rate of Substitution“ (TRS) ist die Steigung der Isoquante. Sie gibt an, in welchem Verhältnis 2 Inputfaktoren substituierbar sind, ohne dass sich die Outputmenge, ändert.

Klingt erstmal schwer, ist aber eigentlich ganz einfach. Da sich die Inputfaktoren von vorhin für eine Erklärung nicht ganz eignen, nehmen wir uns hier etwas andere Inputfaktoren zur Hilfe: Gehen wir also wieder von der Weinproduktion aus. Diese braucht für das Abfüllen von Weinflaschen Arbeiter und Maschinen. Da Maschinen meist schneller als Menschen arbeiten können, nehmen wir einfach an, dass eine Maschine in der gleichen Zeit doppelt so viele Weinflaschen abfüllt wie ein Arbeiter. Das Austauschverhältnis ist also 1:2 bzw. $\frac{1}{2}$ .

Grenzrate der technischen Substitution, — Grenzrate der technischen Substitution

Die Steigung der Isoquante wäre dann -2 in diesem Punkt. Diese ändert sich aber natürlich je nachdem wo Du Dich auf der Isoquante befindest. Wichtig ist, dass die Grenzrate der technischen Substitution immer negativ ist, was Du an dem fallenden Verlauf der Isoquante erkennen kannst.

Im Video siehst du an den roten Tangenten, in welchen Verhältnis du Arbeiter und Maschinen gegeneinander austauschen könntest, um trotzdem noch die gleiche Outputmenge zu erhalten also auf der gleichen Isoquante zu bleiben. Die Grenzrate der technischen Substitution hat aber natürlich in beiden Punkten verschiedene Werte.
Im oberen Punkt hast du wesentlich mehr Maschinen als Arbeiter für das Abfüllen der Weinflaschen eingeplant. Da Dir eben wenige Arbeiter zur Verfügung stehen, musst Du umso mehr Maschinen einsetzten, um auf die gleiche Outputmenge zu kommen. Im unteren Punkt ist es genau umgekehrt.

Grenzrate der technischen Substitution: Beispiel

Schauen wir uns das Ganze mal rechnerisch an: Zunächst brauchst Du natürlich wieder eine Produktionsfunktion, wir nehmen eine Funktion imperfekter Substitute:

$y\left(x_{1,}x_2\right)={x_1}^\frac{1}{2}\ast{x_2}^\frac{1}{3}$

Für die Grenzrate der technischen Substitution musst Du auch hier wieder den Grenznutzen ausrechnen. Nur diesmal von beiden Gütern. Du leitest die Produktionsfunktion also einmal nach x_1 und einmal nach x_2 ab. Damit erhältst Du das Grenzprodukt der Arbeit (für Arbeiter):

${MP}_1=\ \frac{1}{2}{x_1}^{-\frac{1}{2\ \ }}*{x_2}^\frac{1}{3}$

und für Kapital (Maschinen)

${MP}_2=\ \frac{1}{3}{x_1}^\frac{1}{2\ \ }*{x_2}^{-\frac{2}{3}}$

Um dann die Grenzrate der technischen Substitution auszurechnen, musst Du nur noch die Grenzprodukte durcheinander teilen. Also

$\frac{{MP}_1}{{MP}_2} = -\frac{3}{2\ }\ast\frac{x_2}{x_1}$

Wenn du jetzt auch noch Werte für x_1 und x_2 gegeben hast, kannst Du durch Einsetzten auch schon ein konkretes Austauschverhältnis berechnen.
Nehmen wir z. B. an, Du hast ein Inputfaktorbündel

$X^{1\ }=\ \left\{x_1=9,\ x_2=8\ \right\}$

Das heißt, Du hast 9 Arbeiter eingestellt und 8 Maschinen in Betrieb, dann wäre Dein Austauschverhältnis durch Einsetzten in Deine ausgerechnete Grenzrate der technischen Substitution = $-\frac{4}{3}$ . Du würdest also 4 Maschinen für 3 Arbeiter tauschen. Hier scheinen also die Arbeiter eine höhere Outputmenge zu produzieren als die Maschinen. Besser zu verstehen ist das vielleicht, wenn Du Dir auch das einmal graphisch anschaust:

Grenzrate der technischen Substitution Beispiel, Grenzrate der technischen Substitution berechnen — Grenzrate der technischen Substitution Beispiel

Hier siehst Du, dass Du zu Beginn eben 9 Arbeiter eingestellt hast und 8 Maschinen besitzt. Deine Grenzrate der technischen Substitution ist also $-\frac{4}{3}$ .

Zusammenfassung

Um zu erfahren, wie sich die Outputmenge in Abhängigkeit eines Inputfaktors verändert, berechnest Du das Grenzprodukt. Dieses lässt sich ganz leicht durch das Ableiten der Produktionsfunktion nach einem der beiden Inputfaktoren ermitteln. Etwas komplizierter ist die Grenzrate der technischen Substitution: Sie gibt Dir das Austauschverhältnis zweier Inputfaktoren an durch das Du die gleiche Produktionsmenge erhältst, also auf der gleichen Isoquante bleibst. Die Grenzrate der technischen Substitution errechnest Du Dir einfach indem Du die beiden Grenzprodukte in ein Verhältnis setzt, also dividierst, und dann die Werte Deines Faktorbündels einsetzt.

Beliebte Inhalte aus dem Bereich Mikroökonomie

Intro Mikroökonomie Unternehmen

Produktionsfunktionen und Isoquanten

Grenzprodukt und Grenzrate der technischen Substitution

Kurzfristige Gewinnmaximierung

Langfristige Gewinnmaximierung

Kurzfristige Kostenminimierung

Langfristige Kostenminimierung

Angebotsfunktion und langfristige Preisuntegrenze

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .