Video

Taylorreihen – Anwendung

Da du nun weißt, wie du theoretisch eine Taylorreihe entwickeln kannst, wollen wir uns das Ganze nun noch an mehreren Beispielen anschauen.

Inhaltsübersicht

Taylor Entwicklung: Taylorreihe Beispiel

Im Folgenden betrachten wir zunächst das Beispiel der Funktion $\frac{1}{1-x}$ . Wir können Taylorreihen berechnen, um zu verstehen, wo der Grenzwert der geometrischen Reihe herkommt. Die geometrische Reihe ist die Reihe von x^n und ihr Grenzwert ist $\frac{1}{1-x}$ .

Thermodynamische Systeme Herunterladen

$G=\sum_{n=0}^{\infty}x^n=1+x+x^2+x^3+\ldots$

$G=\sum_{n=0}^{\infty}x^n=1+x+x^2+x^3+\ldots=\frac{1}{1-x}$

Also bestimmen wir die Taylorreihe der Funktion $f\left(x\right)=\frac{1}{1-x}$ . Wir erinnern uns an die Definition der Taylor-Reihe:

$T_mf\left(x\right):=\sum_{n=0}^{m-1} \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n$

Nun wählen wir den Entwicklungspunkt x_0=0 und bilden die ersten drei Ableitungen in die wir für x_0 einsetzen. Wenn du dir die ersten drei Ableitungen einmal genauer anschaust, erkennst du ein Muster und kannst damit alle n-ten Ableitungen aufstellen.

Taylorreihen Beispiele — Taylorreihen Beispiele: Ableitungen

Mit diesen Ableitungen kannst du ohne Probleme die Koeffizienten 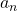a_n bestimmen, indem du sie durch teilst:

$a_n :=\frac{f^{(n)}(x_0)}{n!}=\frac{n!}{(1-x_0)^{(n+1)}n!}$

$a_n:=\frac{n!}{(1-x_0)^{(n+1)}n!}=\frac{1}{1}=1$

kürzt sich raus. Die Koeffizienten ergeben sich zu 1 und die Taylorreihe ist:

Taylorreihe Beispiele

Nach Einsetzen von 1 für die Koeffizienten und 0 für den Entwicklungspunkt x_0 resultiert die Summe von x^n . Das ist genau die geometrische Reihe.

Hiermit hast du bewiesen, dass der Grenzwert der geometrischen Reihe $\sum_{n=1}^{\infty}x^n=\frac{1}{1-x}$ ist.

Rechenregeln Taylor Reihe

Kommen wir jetzt zu ein paar Rechenregeln, die für Taylorreihen gelten:

$T\left(f+g\right)=Tf+Tg$

1. Die Taylorreihe der Summe von f und g ist die Summe der Taylorreihen von f und g.

$T\left(f\ast\ g\right)=Tf\ast\ Tg$

2.Die Taylorreihe des Produkts von f und g ist das Produkt der Taylorreihen von f und g.

$T\left(f^\prime\right)=\left(Tf\right)^\prime$

3.Die Taylorreihe der Ableitung von f, also von f‘, ist die Ableitung der Taylorreihe von f.

$T\left(\int f\right)=\int\left(Tf\right)$

4.Die Taylorreihe des Integrals von f ist das Integral der Taylorreihe an f.

Taylorreihen Rechenregeln

Diese Regeln können an vielen Stellen hilfreich sein. Betrachten wir wieder unser Beispiel von oben. Integriert man nun die geometrische Reihe kommt man auf dieses Ergebnis:

$-\ln{\left(1-t\right)}=\ t+\frac{1}{2}t^2+\frac{1}{3}t^3+\ldots$

Darauf können wir nun die oben aufgeführte Rechenregel zu Integralen von Taylorreihen anwenden:

$T\int_{0}^{t}f\left(x\right)dx=\int_{0}^{t}Tf\left(x\right)dx$

Die Integralgrenzen entsprechen denen der ursprünglichen Aufgabenstellung. Null ist die Untergrenze und ein beliebiges t die Obergrenze. Wir wenden dann die Integralregel an. Jetzt setzen wir die Taylorreihe von $\frac{1}{1-x}$ ein, die wir am Anfang des Beitrags berechnet haben. Die Integration von Polynomen kennst du ja. Das Integral von 1 ist , das von ist $\frac{1}{2}x^2$ und so weiter.

Taylorreihen: Amwendung Rechenregeln

Jetzt setzt du noch die Grenzen ein und erhältst genau das Taylorpolynom, das wir erwartet haben:

$-\ln{\left(1-t\right)}=\ t+\frac{1}{2}t^2+\frac{1}{3}t^3+\ldots$

Wichtige Taylorreihen

Als Nächstes zeigen wir dir ein paar wichtige Taylorreihen und wie du diese nutzen kannst:

Wichtige Taylorreihen

Das Beispiel zur Taylorreihe des Sinus kannst du dir ebenfalls in einem Video ansehen. Der Cosinus ist analog und besteht nur aus geraden Funktionen. Die Taylorreihe der e-Funktion ist die Summe über 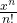$\frac{x^n}{n!}$ . Auch $\frac{1}{1-x}$ haben wir uns am Anfang des Beitrags ausführlich angeschaut. Beachte, dass hier der Definitionsbereich auf -1, 1 eingeschränkt ist.

Verwendung Taylorreihen zur Entwicklung Taylorpolynome: Taylorreihe Tangens

Diese Taylorreihen sind einfach und wir können sie nutzen, um Taylorpolynome komplizierterer Funktionen aufzustellen. Genau das zeigen wir dir jetzt. Wir wollen das Taylor-Polynom $T_6f\tan{(x)}$ bestimmen. Dafür verwenden wir nur bereits bekannte Taylorreihen. Du weißt, dass sich der Tangens als Quotient von Sinus und Kosinus darstellen lässt. Ersetze nun den Sinus und den Kosinus durch ihre Taylorreihen und substituiere $u=\frac{x^2}{2}-\frac{x^4}{24}+O\left(x^6\right)$ . Von $\frac{1}{1-u}$ kennst du das Taylor-Polynom bereits und kannst den Ausdruck ersetzen.

Taylorpolynom Tangens

Jetzt kannst du bis zur Ordnung fünf ausmultiplizieren. Du brauchst nur die Potenzen bis zur Ordnung fünf, da du T_6f berechnest. Dass wir nur ungerade Exponenten haben, ist ein gutes Zeichen, da der Tangens eine ungerade Funktion ist. Ab der siebten Ordnung fassen wir die Terme im Landau-Symbol zusammen. Jetzt noch zusammenfassen und du erhältst das Ergebnis:

$\tan{\left(x\right)}=x+\frac{x^3}{3}+\frac{2x^5}{15}+O\left(x^7\right)$

Das Taylorpolynom sechster Ordnung sieht also wie folgt aus:

$T_6f(x)=x+\frac{x^3}{3}+\frac{2x^5}{15}$

Und so kannst du Taylorpolynome berechnen, ohne komplizierte Ableitungen des Tangens berechnen zu müssen.

Beliebte Inhalte aus dem Bereich Mathe für Ingenieure

Intro Funktionenreihen

Funktionenfolgen - punktweise Konvergenz

Funktionenfolgen - gleichmäßige Konvergenz

Funktionenreihen

Taylorreihen - Landausymbol

Taylorreihen - Anwendung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .