Video

Klassifizierung partieller Differentialgleichungen

Partielle Differentialgleichungen sind ein wichtiges Thema im Maschinenbau. In diesem Beitrag erklären wir dir, was sie sind und in welche Klassen du sie einteilen kannst.

Inhaltsübersicht

Partielle DGL 2. Ordnung

Partielle Differentialgleichungen sind Differentialgleichungen, die zum Teil aus partiellen Ableitungen bestehen. Du kannst sie zum Beispiel benutzen, um physikalische Vorgänge mathematisch darzustellen. Zu Beginn musst du erst einmal lernen, wie du partielle Differentialgleichungen zweiter Ordnung klassifizierst. Liegt dir eine partielle Differentialgleichung vor und ist sie linear und von zweiter Ordnung, dann kannst du ihren Typ bestimmen. Du erinnerst dich: Die höchste vorkommende Ableitung gibt die Ordnung deiner DGL an. Allgemein sieht eine partielle Differentialgleichung zweiter Ordnung so aus:

$\sum_{i,j=1}^{d}{A_{ij}(\mathbit{x})\partial_{x_i}\partial_{x_j}u(\mathbit{x})}+\sum_{i=1}^{d}{b_i(\mathbit{x})\partial_{x_i}u(\mathbit{x})}+c\left(\mathbit{x}\right)u\left(\mathbit{x}\right)=f(\mathbit{x})$

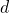steht für Dimension und gibt die Anzahl der Variablen an, von denen die Funktion u abhängt.

$u=u\left(\mathbit{x}\right),\ \mathbit{x}\in R^d$

Wenn 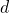gleich zwei ist, ist von zwei Variablen abhängig.

u=u(x_1,x_2)

Kommen wir zurück auf die Darstellung der partiellen Differentialgleichung. A_i_j sind die Koeffizienten der zweiten Ableitungen, b_i sind die Koeffizienten der ersten Ableitungen und c der Koeffizient der unabgeleiteten Funktion . Diese Koeffizienten können alle von den Variablen im Vektor abhängen.

Vektor x bei differentialgleichungen — Bildung von Vektor x

Allgemeine Schreibweise in zweidimensionale DGL umwandeln

Lass dich von den Summen und Indizes nicht verunsichern. Denn jetzt zeigen wir dir, wie du von der allgemeinen Schreibweise auf eine zweidimensionale Differentialgleichung übergehst.

$\sum_{i,j=1}^{2}{A_{ij}\left(\mathbit{x}\right)\partial_{x_i}\partial_{x_j}u\left(\mathbit{x}\right)}+\sum_{i=1}^{2}{b_i\left(\mathbit{x}\right)\partial_{x_i}u\left(\mathbit{x}\right)}+c\left(\mathbit{x}\right)u\left(\mathbit{x}\right)=f\left(\mathbit{x}\right)$

Zunächst schreiben wir die erste Summe aus. Dafür musst du für und einfach Eins beziehungsweise Zwei einsetzen und alle Kombinationen durchgehen.

$A_{11}(x_1,x_2)\partial_{x_1}\partial_{x_1}u\left(x_1,x_2\right)+A_{12}(x_1,x_2)\partial_{x_1}\partial_{x_2}u\left(x_1,x_2\right)+A_{21}(x_1,x_2)\partial_{x_2}\partial_{x_1}u\left(x_1,x_2\right)+A_{22}(x_1,x_2)\partial_{x_2}\partial_{x_2}u\left(x_1,x_2\right)+\sum_{i=1}^{2}{b_i(\mathbit{x})\partial_{x_i}u(\mathbit{x})}+c\left(\mathbit{x}\right)u\left(\mathbit{x}\right)=f(\mathbit{x})$

Wir schreiben diesen Teil mal etwas übersichtlicher, indem wir alle Abhängigkeiten in Klammern weglassen und die partiellen Ableitungen durch Indizes ersetzen.

$A_{11}u_{xx}+2A_{12}u_{xy}+A_{22}u_{yy}+\sum_{i=1}^{2}{b_i\left(\mathbit{x}\right)\partial_{x_i}u\left(\mathbit{x}\right)}+c\left(\mathbit{x}\right)u\left(\mathbit{x}\right)=f\left(\mathbit{x}\right)$

x_1 benennen wir um in und x_2 in . $A_{12}$ und $A_{21}$ sind aufgrund des Satzes von Schwarz gleich.

$A_{12}=A_{21}$

Auf die gleiche Art und Weise schreiben wir den Rest der Gleichung aus.

$A_{11}u_{xx}+2A_{12}u_{xy}+A_{22}u_{yy}+b_1u_x+b_2u_y+cu=f(x,y)$

Sieht doch gar nicht mehr so schlimm aus! Um jetzt den Typ zu bestimmen, musst du die Koeffizienten A_i_j in einer Matrix zusammenfassen. Diese ist per Definition symmetrisch.

$\mathbit{A}=\left[\begin{matrix}A_{11}&A_{12}\\A_{12}&A_{22}\\\end{matrix}\right]$

Die Koeffizienten b_i ergeben einen Vektor.

$\mathbit{b}=\left[\begin{matrix}b_1\\b_2\\\end{matrix}\right]$

Im nächsten Schritt bestimmst du die Eigenwerte von A.

Eigenwerte bei partiellen Differentialgleichungen bestimmen — Eigenwerte bestimmen

Die Differentialgleichung ist elliptisch, wenn A positiv definit ist, also alle Eigenwerte positiv sind. Sie ist hyperbolisch, wenn alle Eigenwerte außer einem positiv sind und der übrige Eigenwert negativ ist. Die Differentialgleichung ist parabolisch, wenn alle Eigenwerte von A außer einem positiv sind und der letzte Eigenwert gleich Null ist. Außerdem muss die Matrix $\left[\mathbit{A}\middle|\mathbit{b}\right]$ vollen Rang haben. Diese Überprüfung wird oft vergessen.

Beispiele

Jetzt wollen wir uns mal ein paar Beispiele ansehen. Zunächst schauen wir uns die Poisson-Gleichung an:

$-\Delta u\left(\mathbit{x}\right)=f(\mathbit{x})$

Das Dreieck ist der Laplace-Operator. Er ist wie folgt definiert:

$\Delta u(\mathbit{x},t)=\sum_{i=1}^{d}\frac{\partial^2u\left(\mathbit{x},t\right)}{\partial\ x_i^2}$

Die zweiten Ableitungen nach allen Variablen im Vektor x werden summiert. Im Zweidimensionalen sieht die Poisson-Gleichung so aus:

$-\partial_{xx}u-\partial_{yy}u=f(x,y)$

Von dieser wollen wir die Matrix A bestimmen:

$\mathbit{A}=\left[\begin{matrix}-1&0\\0&-1\\\end{matrix}\right]$

Der Vorfaktor der zweiten Ableitung nach x kommt an die Stelle Eins Eins der Matrix und der Vorfaktor der zweiten Ableitung nach y an die Stelle Zwei Zwei. Gemischte Ableitungen kommen nicht vor, so dass wir an den restlichen Stellen Nullen eintragen. Es ergibt sich eine Diagonalmatrix, so dass wir die Eigenwerte einfach ablesen können. Beide Eigenwerte haben den Wert minus Eins und sind damit negativ. Folglich wäre die Differentialgleichung keine der drei Typen. Man hätte die DGL aber auch schon zu Beginn mit minus Eins durchmultiplizieren können und dann durch aufstellen von A die Einheitsmatrix erhalten.

Beispiel

Diese hat die positiven Eigenwerte Eins und Eins. Die Poisson-Gleichung ist also elliptisch. Im Zweidimensionalen kannst du auch an der Determinante sehen, welcher Typ vorliegt.

$\det{\mathbit{A}}=-1\ast \left(-1\right)=1>0$

Ist die Determinante positiv, ist die Differentialgleichung elliptisch. Das kann dir helfen, wenn du keine einfache Diagonalmatrix hast.

Eindimensionale Wärmeleitungsgleichung

Als Nächstes nehmen wir uns die eindimensionale Wärmeleitungsgleichung vor. Als zweite Dimension kommt jetzt noch die Zeit ins Spiel.

$\partial_tu\left(x,t\right)=\partial_{xx}u(x,t)$

Wir stellen die Gleichung etwas um

$\partial_{xx}u\left(x,t\right)-\partial_tu\left(x,t\right)=0$

und stellen die Matrix A auf.

$A=\left[\begin{matrix}1&0\\0&0\\\end{matrix}\right]$

Es kommt nur die zweite Ableitung nach x vor, also tragen wir eine Eins ein. Es gibt aber keine zweite Ableitung nach t oder gemischte Ableitungen. Folglich füllen wir die Matrix mit Nullen auf. Es ergibt sich wieder eine Diagonalmatrix, sodass wir die Eigenwerte Eins und Null ablesen können. Diese Eigenwerte deuten darauf hin, dass die Differentialgleichung parabolisch ist. Bei parabolischen Differentialgleichungen musst du noch prüfen, ob die zusammengesetzte Matrix $\left[\mathbit{A}\middle|\mathbit{b}\right]$ vollen Rang hat. Dafür stellen wir b auf. Auch das kannst du aus der DGL ablesen, und zwar an den Vorfaktoren vor den ersten Ableitungen

$b=\left[\begin{matrix}0\\-1\\\end{matrix}\right]$

Es wird einfach nach t abgeleitet, aber nicht nach x. Die Matrix $\left[\mathbit{A}\middle|\mathbit{b}\right]$ sieht also so aus

$\left[\mathbit{A}\middle|\mathbit{b}\right]=\left[\begin{matrix}1&0&0\\0&0&-1\\\end{matrix}\right]$

Die Zeilen sind linear unabhängig und damit hat die Matrix vollen Rang. Also ist die Wärmeleitungsgleichung parabolisch. Für 2×2-Matrizen parabolischer Differentialgleichungen ist übrigens die Determinante gleich Null.

$\det{\mathbit{A}}=-1\ast0=0$

Das ist hier der Fall. Aber du hättest danach dennoch den Rang der $\left[\mathbit{A}\middle|\mathbit{b}\right]$ -Matrix überprüfen müssen.

Eindimensionale Wellengleichung

Als letztes schauen wir uns die eindimensionale Wellengleichung an. Diese ist ebenso von der Zeit t abhängig.

$\partial_{tt}u\left(x,t\right)=\partial_{xx}u(x,t)$

Wir stellen die Gleichung um

$\partial_{xx}u\left(x,t\right)-\partial_{tt}u\left(x,t\right)=0$

Und bestimmen die A-Matrix

$\mathbit{A}=\left[\begin{matrix}1&0\\0&-1\\\end{matrix}\right]$

Die Eigenwerte stehen auch hier auf der Diagonalen. Es sind Eins und minus Eins und damit ist die Wellengleichung hyperbolisch. Alternativ hättest du auch hier die Determinante bestimmen können, da die A-Matrix eine 2×2-Matrix ist.

$\det{\mathbit{A}}=-1\ast1=-1$

Sie ist negativ. Auch daraus hättest du folgern können, dass die Differentialgleichung hyperbolisch ist.
Fassen wir die Kriterien noch einmal zusammen. Die Matrix A elliptischer Differentialgleichungen hat nur positive Eigenwerte, sie ist also positiv definit. Die Determinante der A-Matrix ist größer Null, wenn es eine Zwei-Kreuz-Zwei-Matrix ist und ein Beispiel für eine elliptische Gleichung ist die Poisson-Gleichung. Hyperbolische Differentialgleichungen haben d minus Eins positive und einen negativen Eigenwert, sodass die A-Matrix indefinit ist. Im Zweidimensionalen ist die Determinante kleiner Null. Ein Beispiel ist die Wellengleichung. Parabolische DGLs haben d minus Eins positive Eigenwerte und einen Eigenwert gleich Null. Damit sind sie positiv semidefinit und die Determinante ist gleich Null. Außerdem musst du prüfen, ob die Matrix A b vollen Rang hat. Ein Beispiel ist die Wärmeleitungsgleichung.

Klassen zweidimensionaler DGLs — Klassen

Jetzt weißt du, wie du partielle DGLs in elliptische, hyperbolische und parabolische Differentialgleichungen einteilst. In den nächsten Beiträgen lernst du die verschiedenen Typen zu lösen.

Beliebte Inhalte aus dem Bereich Mathe für Ingenieure

Intro Partielle DGL lösen

Klassifizierung partieller Differentialgleichungen

Separationsansatz

Wärmeleitungsgleichung

Wellengleichung

Laplace-Gleichung

Poisson-Gleichung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .