Laplace Gleichung
Du weißt jetzt schon, was partielle Differentialgleichungen sind und wie du diese lösen kannst. In diesem Beitrag wollen wir dein theoretisches Wissen anwenden und uns die Laplace Gleichung anschauen.
Inhaltsübersicht
Die Laplace-Gleichung mit Separationsansatz lösen
Die nach dem 1749 geborenen Mathematiker Pierre-Simon Laplace benannte Gleichung ist eine elliptische partielle Differentialgleichung zweiter Ordnung. Die Laplace Gleichung findet auch in der Physik Anwendung. Sie lässt sich zum Beispiel aus der Wärmeleitungsgleichung herleiten. Hier lösen wir die Laplace-Gleichung auf dem Einheitsquadrat. Dafür verwenden wir den Separationsansatz.
Laplace Gleichung Beispiel

ist die homogene Poisson-Gleichung,

Beides sind elliptische Differentialgleichungen. Wir wollen uns die zweidimensionale Laplace-Gleichung

auf dem Einheitsquadrat ansehen.

Das große 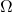 beschreibt das Gebiet, auf dem wir die Differentialgleichung betrachten. In diesem Fall also das Einheitsquadrat.
beschreibt das Gebiet, auf dem wir die Differentialgleichung betrachten. In diesem Fall also das Einheitsquadrat.
Die Randbedingungen sind folgende:
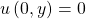



Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Laplace Gleichung Lösen
Wie gewohnt wählst du einen Produktansatz

Und erhältst daraus nach Einsetzen,

Sortieren und Gleichsetzen mit der Konstanten 

zwei gewöhnliche Differentialgleichungen.


Gewöhnliche DGL lösen
Jetzt musst du die gewöhnlichen Differentialgleichungen lösen. Aber mit welcher fängst du an? Du kannst etwas Zeit sparen, wenn du dir die Randbedingungen ansiehst.

sticht heraus. Es ist nicht gleich Null wie die anderen Randbedingungen, sondern gleich  . Also muss der von y abhängige Anteil groß Y eine trigonometrische Funktion sein. Das ist der Fall, wenn
. Also muss der von y abhängige Anteil groß Y eine trigonometrische Funktion sein. Das ist der Fall, wenn  kleiner Null ist.
kleiner Null ist.
Dafür definieren wir ein  ,
,

setzen es in die y-DGL ein


und stellen das charakteristische Polynom auf

Daraus ergeben sich die Eigenwerte,

sodass die Lösungen so aussehen.

Randbedingungen einsetzen
Wie erwartet ist es eine trigonometrische Funktion. Jetzt prüfen wir die Randbedingungen. Diese schreiben wir zunächst für groß Y auf.


Die erste Randbedingung führt auf

Die zweite Randbedingung führt auf

Entweder  ist gleich Null, was aber die triviale Lösung wäre, oder auf
ist gleich Null, was aber die triviale Lösung wäre, oder auf  ist gleich Null. Das ist der Fall, wenn
ist gleich Null. Das ist der Fall, wenn  ein Vielfaches von
ein Vielfaches von  ist.
ist.

Es führt auf die Lösungen

Betrachten wir nun die Differentialgleichung für x.

Hier können wir  für
für  einsetzen,
einsetzen,


die Gleichung umstellen

und das charakteristische Polynom aufstellen.

Es ergeben sich die reellen Eigenwerte

Die Lösung setzt sich also aus zwei Exponentialfunktionen zusammen.

Aus der ersten Randbedingung

folgt,

dass

ist, sodass wir die Lösung in den Sinus Hyperbolicus

umschreiben können. Zur Erinnerung: Der Sinus Hyperbolicus ist  .
.

Wir setzen also für  minus
minus  ein und Klammern Zwei
ein und Klammern Zwei  aus. Übrig bleibt genau der Sinus Hyperbolicus. Damit ist die allgemeine Lösung
aus. Übrig bleibt genau der Sinus Hyperbolicus. Damit ist die allgemeine Lösung

die Summe über n des Produktes aus der Sinus Hyperbolicus-Funktion und der Sinus-Funktion. Mit der letzten Randbedingung

ergibt sich (1)
1: 
2: 
zunächst, dass alle Koeffizienten 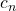 außer
außer  gleich Null
gleich Null 
sind (2). Auflösen der übrigen Gleichung nach  ergibt
ergibt

Jetzt kannst du die Konstante einsetzen und die finale Lösung sieht schließlich so aus.

Damit hast du die Laplace-Gleichung auf dem Einheitsquadrat gelöst. Im nächsten Beitrag lösen wir noch die Poisson-Gleichung.


