Lineare & nichtlineare DGL
Du möchtest den Unterschied zwischen linearen und nichtlinearen Differentialgleichungen kennen lernen und wissen, was es mit den linearen Differentialgleichungen mit konstanten Koeffizienten auf sich hat? Dann bist du hier genau richtig!
Inhaltsübersicht
Unterschied nichtlineare und lineare Differentialgleichung
Beginnen wir mit den linearen Differentialgleichungen. Man bezeichnet eine DGL als linear, wenn sie in folgender Form dargestellt werden kann:

Die Ableitungen werden mit Koeffizienten multipliziert und summiert. Die Koeffizienten können von x abhängen. Kannst du die DGL nicht so darstellen und steckt y oder eine seiner Ableitungen in einer nichtlinearen Funktion, heißt sie nichtlinear.
Beispiele für nichtlineare und lineare Differentialgleichung
Schauen wir uns als nächstes zwei Beispiele an:

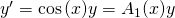
Bei der ersten Gleichung handelt es sich um eine lineare Differentialgleichung. In der zweiten Gleichung siehst du, dass gilt: 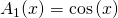 .
.  ist somit ein nichtlinearer Koeffizient.
ist somit ein nichtlinearer Koeffizient.
Schauen wir uns eine weitere Gleichung an:

Hierbei handelt es sich um eine nichtlineare Differentialgleichung, denn hier ist y das Argument der nichtlinearen Kosinusfunktion, es steckt also selbst im Kosinus.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lineare DGL mit konstanten Koeffizienten – ein wichtiger Sonderfall
Bei linearen Differentialgleichungen mit konstanten Koeffizienten, hängen die Koeffizienten  nicht von
nicht von  ab.
ab.

Auch hier ist ein Beispiel hilfreich, um das Thema besser zu verstehen.
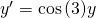
Der Koeffizient  = cos(3) ist nicht von x abhängig und es folgt:
= cos(3) ist nicht von x abhängig und es folgt:

Jetzt hast du auch den Unterschied zwischen linearen und nichtlinearen Differentialgleichungen kennen gelernt und weißt, was lineare Differentialgleichungen mit konstanten Koeffizienten sind.


