Dehnungen
Dehnungen kommen in der Festigkeitslehre vor, wenn eine Kraft auf einen Körper wirkt. Was genau damit gemeint ist und wie du die Dehnungen von Körpern berechnest, erklären wir dir in diesem Beitrag.
Inhaltsübersicht
Die Dehnung von Körpern
Die Dehnung beschreiben wir in der Mechanik mit dem Symbol  . Wir definieren es als:
. Wir definieren es als:

Dabei beschreibt 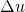 die Längenänderung in die jeweilige Richtung.
die Längenänderung in die jeweilige Richtung.  kann die Länge, Breite oder Dicke des Objekts sein. Stell dir dafür einfach mal ein gespanntes Seil vor. Wenn du noch ein wenig mehr an diesem Seil ziehst, wird es ein wenig länger. Und genau diese Änderung beschreibt
kann die Länge, Breite oder Dicke des Objekts sein. Stell dir dafür einfach mal ein gespanntes Seil vor. Wenn du noch ein wenig mehr an diesem Seil ziehst, wird es ein wenig länger. Und genau diese Änderung beschreibt 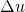 .
.  ist in diesem Fall die Länge
ist in diesem Fall die Länge 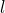 . Genauso kannst du das also in jede Koordinatenrichtung machen. Für einen Balken der Länge
. Genauso kannst du das also in jede Koordinatenrichtung machen. Für einen Balken der Länge 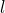 , der Breite
, der Breite  und der Höhe
und der Höhe  ergibt sich also:
ergibt sich also:
Da  unabhängig von der absoluten Länge ist, lassen sich Dehnungen von unterschiedlichen Körpern gut vergleichen.
unabhängig von der absoluten Länge ist, lassen sich Dehnungen von unterschiedlichen Körpern gut vergleichen.
Normaldehnungen
Du hast vielleicht gemerkt, dass wir die Dehnungen doppelt indiziert haben. Das könnte dir aus dem Video Spannungstensor und Spannungszustände bekannt vorkommen. Wir betrachten also Normaldehnungen. Das sind Dehnungen, die in gleiche Richtung gehen, wie der Normalenvektor. Ziehen wir an einem Seil geht der Normalenvektor der Fläche genau in x-Richtung und wir ziehen auch in x-Richtung. Damit können wir von Normaldehnungen ausgehen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Scherdehnungen
Du kannst dir sicher denken, dass es dann auch andere Dehnungen geben muss. Diese werden Scherdehnungen genannt. Wie kann man sich diese jetzt vorstellen? Wir schauen uns dazu einen rechteckigen Balkenquerschnitt an und belasten ihn mit einem Torsionsmoment. Was das genau ist erfährst du im Video zum Zug- und Torsionsversuch. Dieses Moment sorgt jetzt für eine Verdrehung des Querschnitts. Wir dehnen den Querschnitt zwar, aber nicht in Richtung der Achse und damit auch nicht in Richtung der Flächennormalen. Da wir uns im dreidimensionalen Raum befinden, können wir solche Dehnungen in jede Richtung finden. Wir definieren uns also Dehnungen für solche Belastungsfälle in der Mechanik zu:
Doch wie messen wir diese Dehnungen jetzt? Bei Normaldehnungen ist das ja eigentlich einfach, aber hier wirkt das ganze schon aufwändiger. Dafür wird der sogenannte Scherwinkel eingeführt. Um dir diesen näher zu bringen, schauen wir uns wieder den Rechteckquerschnitt unter Torsion an. Durch die Verdrehung, können wir einen Winkel erkennen, um den dieser verdreht wird. Und genau das ist der Scherwinkel. Wir definieren diesen als:
Volumenänderungen
Als letztes wollen wir noch die sogenannte Volumenänderung betrachten. Dazu stellen wir uns einen Schwamm vor: Drückst du diesen zusammen, verringerst du das Volumen. Wir haben also Dehnungen in x, y und z-Richtung. Um uns Arbeit zu sparen, können wir eine gesamte Volumendehnung definieren, als:

Für unseren Schwamm heißt das: Wir bestimmen das ursprüngliche Volumen und danach das Volumen, wenn wir diesen zusammendrücken und erhalten die Dehnung.
Jetzt weißt du was Dehnungen sind und wie du sie selbst bestimmen kannst.


