Gleichungsverfahren

Gleichungsverfahren Kostenrechnung

Das Gleichungsverfahren wird auch Simultanverfahren oder mathematisches Verfahren genannt. Es dient in der Kostenstellenrechnung bzw. allgemein in der Kosten- und Leistungsrechnung (KLR) als Verfahren zur Bestimmung der exakten Werte der innerbetrieblichen Verrechnungspreise, bei dem auch wechselseitige Leistungsbeziehungen zwischen den Vorkosten- und den Endkostenstellen berücksichtigt werden. Um diese komplizierten Leistungsbeziehungen zu berechnen, stellt man ein lineares Gleichungssystem auf. Innerhalb des Gleichungssystems erhält jede Kostenstelle eine eigene Gleichung.

Die grundlegende Gleichungsstruktur sieht folgendermaßen aus:

Wert der abgegebenen Leistungen = primäre Stellenkosten + Wert der empfangenen Leistungen

Beim Gleichungsverfahren ist es, so wie auch bei den anderen Verfahren der Kostenstellenrechnung wichtig, zwischen Hilfskostenstellen bzw. Vorkostenstellen und Hauptkostenstellen bzw. Endkostenstellen zu unterscheiden.

Die Gleichung sieht in mathematischer Form nochmal ein wenig anders aus:

Um es etwas einfacher zu machen, betrachten wir die Gleichung beispielhaft für eine der Kostenstellen:

direkt ins Video springen

• Das K₁ auf der linken Seite der Gleichung steht für die Summe aus den primären und den sekundären Kosten der Kostenstelle 1. Diese berechnest du, indem du zu den primären Gemeinkosten der Kostenstelle die anteiligen Kosten, die von anderen Kostenstellen auf Kostenstelle 1 übertragen werden, addierst.
• PK₁  steht für die primären Gemeinkosten der Kostenstelle 1
• a₁₂ entspricht dem Anteil der Leistung der an Kostenstelle 1 von Kostenstelle 2 geliefert wird.
• K₂ ist der Wert den wir berechnen wollen, danach müssen wir das Gleichungssystem also lösen.
• Da es ja nicht nur eine, sondern mehrere Kostenstellen gibt, musst du diese Gleichung dann für jede der Kostenstellen aufstellen und das so entstehende Gleichungssystem nach , usw. auflösen.

Im Gegensatz zum Anbauverfahren und Stufenleiterverfahren, gilt hier das Prinzip der exakten Kostenüberwälzung, da hier mit exakten Werten gerechnet wird.

Innerbetriebliche Leistungsverrechnung Gleichungsverfahren

Den innerbetrieblichen Leistungsaustausch beim Gleichungsverfahren zu berücksichtigen ist dahingehend wichtig, da Hilfskostenstellen oft Leistungen anderer Hilfskostenstellen beanspruchen. Hilfskostenstellen liefern beispielsweise für den Produktionsprozess wichtige Infrastrukturleistungen, wie etwa den innerbetriebliche Transport oder die Verwaltung. Liefert also die eine Hilfskostenstelle eine Leistung wie Strom an eine andere Hilfskostenstelle und bezieht beispielsweise gleichzeitig Reparaturleistungen von dieser Kostenstelle, so muss die Verflechtung der ausgetauschten Leistungen beachtet werden.

Gleichungsverfahren einfach erklärt

Das Gleichungsverfahren zielt darauf ab, dass keine Kostenstelle einen Gewinn oder einen Verlust erzielt. Es werden dafür die Erlöse einer Kostenstelle den gesamten Kosten (also den primären und sekundären Kosten) dieser Kostenstelle entgegengesetzt.

Vereinfacht gesagt stellen wir die Gleichung so auf, sodass: Wert Input = Wert Output. Die Leistungen einer Kostenstelle werden als mit den darin enthaltenen Kosten bewertet.

Die Herausforderung ist allerdings, dass wir bei zwei sich beliefernden Kostenstellen bereits eine Gleichung mit zwei Unbekannten erhalten. Sobald sich drei oder mehr Kostenstellen gegenseitig beliefern, wird das Gleichungsverfahren  noch komplizierter und manuell nur noch schwer lösbar.

Gleichungsverfahren Aufgaben

Um das Thema ein bisschen besser zu verstehen, schauen wir uns ein konkretes Beispiel an. Es wird angenommen, dass es zwei Kostenstellen: und 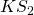gibt. In der Grafik lassen sich deren Leistungsbeziehungen ablesen.

direkt ins Video springen

→ Kostenstelle 1 ()  liefert 40% seiner Leistung an Kostenstelle 2 (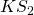) und diese wiederum die Hälfte von deren Leistung an Kostenstelle 1. Der Rest landet auf dem Absatzmarkt.

→ Die primären Gemeinkosten betragen  = 100.000€ und = 150.000€. Um die Endkosten berechnen zu können, brauchen wir zuerst die Summe der Primär- und Sekundärkosten der Kostenstellen. Diese wird K genannt.

Als nächstes müssen die Gleichungen aufgestellt werden.

Wenn wir nun die erste in die zweite für einsetzen, erhalten wir folgendes:

und somit

Wenn wir das wiederum in die erste Gleichung einsetzen, wissen wir, dass  218.750€ beträgt.

direkt ins Video springen

Jetzt müssen wir nur noch die Endkosten auf den jeweiligen Kostenstellen berechnen. Hier zählt wie zuvor nur der Anteil, der letztendlich an den Absatzmarkt abgegeben wird.

• Bei der Kostenstelle 1 bleiben 60% übrig, daher rechnen wir 0,6 x 218.750€ = 131.250€.
• In der Kostenstelle 2 wird die Hälfte der Leistungen abgegeben. Übrig bleiben also 0,5 x 237.500 = 118.750€.
• Wenn du nun beide Endkosten zusammenzählst, erhältst du 131.250€ + 118.750€ = 250.000€.

⇒ Diese Zahl entspricht genau der Summe der primären Gemeinkosten. Das muss immer so sein! So kannst du am Ende überprüfen, ob du mit dem Verfahren richtig gerechnet hast.

Jetzt weißt du genau, was man unter dem Gleichungsverfahren versteht und wie die Sekundärkostenverrechnung in der innerbetrieblichen Leistungsverrechnung mithilfe dieses Verfahrens funktioniert.