Video

Biegelinie berechnen – Dreieckslast

Willst du wissen wie du die Biegung eines Balkens mathematisch beschreiben kannst? Dann bist du hier genau richtig!

Inhaltsübersicht

Biegelinie einer Dreieckslast bestimmen

Um die Biegung des geraden Balkens bei Dreieckslast berechnen zu können, betrachten wir ein Beispiel dazu: Wir haben den gleichen Kragarm wie im Video zur „Biegungslinie – Einzellast“ vorliegen. Zur Erinnerung: Ein Kragarm ist ein Balken, der am linken Rand fest eingespannt ist und am rechten Rand ein freies Ende besitzt. Der betrachtete Balken hat die Länge L gleich ein Meter, den E-Modul E gleich 210.000MPa und das Flächenträgheitsmoment J zwei zwei gleich 290.000 Millimeter hoch vier. Das Koordinatensystem legen wir in die Einspannung, wobei x nach rechts und z nach unten zeigt.

Streckenlast berechnen

Den Balken wollen wir jetzt unter einem zweiten Lastfall betrachten:

Eine Dreieckslast $q_2(x)=q_0(1-\frac{x}{l})$ mit q Null gleich 5 Kilonewton pro Meter.

Dreieckslast

Da wir nun einen Lastverlauf betrachten, können wir die bekannte Formel für die Biegelinie nicht mehr so einfach verwenden. Das liegt daran, dass wir den Momentenverlauf benötigen, wir ihn aber nicht so schnell bestimmen können. Um das Problem zu lösen, denken wir nochmal zurück an die Schnittgrößen: wenn wir den Momentenverlauf zweimal ableiten, erhalten wir die Streckenlast. Das heißt, wir müssen die Biegelinie noch zweimal ableiten und es ergibt sich:

$w^{IV}\left(x\right)=\frac{q(x)}{EJ_{22}}$

Setzen wir die Funktion für die Dreieckslast ein, erhalten wir für die vierte Ableitung:

$w_2^{IV}\left(x\right)=\frac{q\left(x\right)}{EJ_{22}}=\frac{q_0}{EJ_{22}}(1-\frac{x}{l})$

Das integrieren wir nun viermal. Die erste Integration ergibt:

$w_2^{\prime\prime\prime}\left(x\right)=\int{\frac{q_0}{EJ_{22}}(1-\frac{x}{l})\ dx}=\frac{q_0}{EJ_{22}}\left(x-\frac{x^2}{2l}+C_1\right)$

Nach der zweiten Integration erhalten wir:

$W_2^{\prime\prime}\left(x\right)=\int{\frac{q_0}{EJ_{22}}\left(x-\frac{x^2}{2l}+C_1\right)dx}=\frac{q_0}{EJ_{22}}\left(\frac{x^2}{2}-\frac{x^3}{6l}+C_1x+C_2\right)$

Und nach der dritten:

$W_2^\prime\left(x\right)=\int{\frac{q_0}{EJ_{22}}\left(\frac{x^2}{2}-\frac{x^3}{6l}+C_1x+C_2\right)dx}=\frac{q_0}{EJ_{22}}\left(\frac{x^3}{6}-\frac{x^4}{24l}+\frac{C_1x^2}{2}+C_2x+C_3\right)$

Und schließlich ergibt sich w2 von x mit:

$W_2\left(x\right)=\int{\frac{q_0}{EJ_{22}}\left(\frac{x^3}{6}-\frac{x^4}{24l}+\frac{C_1x^2}{2}+C_2x+C_3\right)dx}$

$=\frac{q_0}{EJ_{22}}\left(\frac{x^4}{24}-\frac{x^5}{120l}+\frac{C_1x^3}{6}+\frac{C_2x^2}{2}+C_3x+C_4\right)$

Du siehst: wir erhalten außerdem die vier Integrationskonstanten C eins, C zwei, C drei und C vier.

Randbedingungen

Welche Randbedingungen, können wir jetzt anwenden? Betrachten wir die dritte Ableitung der Biegelinie, erkennst du vielleicht aus den Schnittgrößen, dass es sich um den Querkraftverlauf handelt, wenn wir nicht durch E mal J22 teilen würden. Wir hätten dann also die erste Ableitung des Momentenverlaufs, der schließlich den Querkraftverlauf darstellt.

$\left(M\left(x\right)\right)^\prime=Q\left(x\right)$

Das heißt die dritte Ableitung ist auch Null, wenn der Querkraftverlauf Null ist. In unserem Fall muss die Querkraft am Balkenende, also x gleich L, Null sein. Für die zweite Ableitung wissen wir ja, dass der Momentenverlauf ausschlaggebend ist. Ist jetzt das Moment an einer Stelle gleich Null, ist dann folglich auch die zweite Ableitung der Biegelinie gleich Null. Das finden wir am Balkenende, also bei x gleich L.

Damit erhalten wir für die dritte Ableitung der Biegelinie am Balkenende:

$w_2^{\prime\prime\prime}\left(x=l\right)=\frac{q_0}{EJ_{22}}\left(l-\frac{l^2}{2l}+C_1\right)=0$

Es ergibt sich nun:

$C_1=-l+\frac{l^2}{2l}=-\frac{l}{2}$

Für die zweite Ableitung erhalten wir dann:

$w_2^{\prime\prime}\left(x=l\right)=\frac{q_0}{EJ_{22}}\left(\frac{l^2}{2}-\frac{l^3}{6l}-\frac{l}{2}l+C_2\right)=0$

Stellen wir diese Gleichung jetzt nach C zwei um, erhalten wir:

$C_2=\frac{l^3}{6l}-\frac{l}{2}l+\frac{l^2}{2}=\frac{l^2}{6}$

Damit haben wir die ersten beiden Integrationskonstanten bestimmt. Die anderen beiden ermitteln wir jetzt genauso wie vorher mit der Bedingung, dass an der Einspannung sowohl Biegelinie, als auch Krümmung Null sein müssen. An der Einspannung erhalten wir dann für die Krümmung:

$w_2^\prime\left(x=0\right)=\frac{q_0}{EJ_{22}}\left(\frac{0^3}{6}-\frac{0^4}{24l}-\frac{l0^2}{4}+\frac{l^2}{6}0+C_3\right)=\frac{q_0}{EJ_{22}}C_3=0$

Um die Gleichung zu erfüllen, muss C drei Null sein. An der Einspannung ergibt sich für die Biegelinie:

$w_2\left(x=0\right)=\frac{q_0}{EJ_{22}}\left(\frac{0^4}{24}-\frac{0^5}{120l}-\frac{l0^3}{12}+\frac{l^20^2}{12}+C_4\right)=\frac{q_0}{EJ_{22}}C_4=0$

Damit muss auch C vier gleich Null sein und wir erhalten unsere gesamte Formel für die Biegelinie ohne Werte:

$w_2\left(x\right)=\frac{q_0}{EJ_{22}}\left(\frac{x^4}{24}-\frac{x^5}{120l}-\frac{lx^3}{12}+\frac{l^2x^2}{12}\right)$

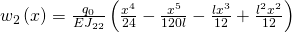
Setzten wir die Werte für L, q Null, E und J zwei zwei ein und ziehen x Quadrat vor die Klammern, erhalten wir:

Endergebnis

So, jetzt weißt du auch wie du vorgehen musst, wenn du es mit einer Streckenlast zu tun bekommst.

Beliebte Inhalte aus dem Bereich Festigkeitslehre

Intro Festigkeitslehre II

Biegung des geraden Balkens

Biegung des geraden Balkens - Einzellast

Biegung des geraden Balkens - Dreieckslast

Schubspannungen - Vollquerschnitte

Schubspannungen - Dünnwandig, offene Querschnitte I

Schubspannungen - Dünnwandig, offene Querschnitte II

Schubspannungen bei Torsion

Torsion - Verdrehwinkel

Eulersche Knickfälle

Eulersche Knickfälle - Übung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .