Video

Biegelinie berechnen – Einzellast

Willst du wissen wie du die Biegung eines Balkens mathematisch beschreiben kannst? Dann bist du hier genau richtig!

Inhaltsübersicht

Biegelinie einer Einzellast bestimmen

Zu Beginn frischen wir noch einmal die Grundlagen auf: Wir betrachten bei der Biegung des geraden Balkens in der Regel die neutrale Faser. Diese erfährt unter Last keine Längenänderung, bleibt also gleich lang. Die Linie folgt allerdings trotzdem der Biegung. Mit ihr können wir dann auch die Veränderung der Lage jedes einzelnen Punktes im Balken beschreiben. Darum wird diese Linie auch Biegelinie genannt. Die Biegelinie können wir in differentieller, also abgeleiteter Form beschreiben durch:

$w^{\prime\prime}\left(x\right)=-\frac{M_y(x)}{EJ_{22}}$

Für das weitere Vorgehen wird diese Gleichung üblicherweise integriert. Nun weißt du sicher noch aus der Schule, dass du beim Integrieren Integrationskonstanten erhältst. Um diese zu bestimmen, verwenden wir Randbedingungen am Balken, die sich nach der Art der Einspannung unterscheiden:

Die Einspannung: Biegelinie w(x) und Krümmung der Biegelinie $w^\prime\left(x\right)$ sind hier Null. Querkraft und Moment sind unbekannt.
Das Festlager: Biegelinie w(x) und Moment sind hier Null, Querkraft und Krümmung $w^\prime\left(x\right)$ sind unbekannt und
Der freie Rand: Biegelinie w(x) und Krümmung $w^\prime\left(x\right)$ sind hier unbekannt. Querkraft und Moment sind Null.

Einspannung

Zusätzlich gibt es noch das Gelenk. Es ist aber für die folgende Beispielaufgabe nicht von Bedeutung.

Biegelinie eines Kragarms bestimmen

Jetzt bist du wieder auf dem aktuellen Stand und wir können unser Beispiel durchrechnen. Dazu betrachten wir einen einfachen Kragarm. Ein Kragarm ist ein Balken, der am linken Rand fest eingespannt ist und am rechten Rand ein freies Ende besitzt. Der betrachtete Balken hat die Länge L gleich ein Meter, den E-Modul E gleich 210.000MPa und das Flächenträgheitsmoment J zwei zwei gleich 290.000 Millimeter hoch vier. Das Koordinatensystem legen wir in die Einspannung, wobei x nach rechts und z nach unten zeigt.
Den Balken wollen wir jetzt unter dem folgenden Lastfall betrachten:
Eine Einzelkraft F gleich 800 Newton greift am Balkenende an.
Für diesen Fall wollen wir nun die Gleichung der Biegelinie bestimmen.

Momentenverlauf

Zu Beginn müssen wir den Momentenverlauf über den Balken mit Hilfe der Schnittgrößen bestimmen. Dieser ergibt sich für uns zu:

$M_1\left(x\right)=-F\left(l-x\right)$

Wenn dir das zu schnell ging, schau dir am besten noch mal das Video zu Schnittgrößen an.

Integrationskonstanten bestimmen

Das setzen wir anschließend in die Gleichung für die zweite Ableitung der Biegelinie ein und erhalten damit:

$w_1^{\prime\prime}\left(x\right)=\frac{F\left(l-x\right)}{EJ_{22}}$

Daraus ergibt sich durch Integration die Krümmung:

$W_1^\prime\left(x\right)=\int{\frac{F\left(l-x\right)}{EJ_{22}}dx}=\frac{F}{EJ_{22}}(lx-\frac{x^2}{2}+C_1)$

Und anschließend durch eine weitere Integration die Biegelinie:

$w_1\left(x\right)=\int{\frac{F}{EJ_{22}}(lx-\frac{x^2}{2}+C_1)dx}=\frac{F}{EJ_{22}}(\frac{lx^2}{2}-\frac{x^3}{6}+C_1x+C_2)$

Die Integrationskonstanten erhalten wir jetzt mit Hilfe der Randbedingungen. Da wir links eine Einspannung haben, wissen wir, dass dort die Krümmung und die Biegelinie gleich Null sein müssen. Damit ergeben sich aus den Randbedingungen zwei Gleichungen:

$w_1^\prime\left(x=0\right)=\frac{F}{EJ_{22}}\left(l0-\frac{0^2}{2}+C_1\right)=0$

$w_1\left(x=0\right)=\frac{F}{EJ_{22}}\left(\frac{l0^2}{2}-\frac{0^3}{6}+C_10+C_2\right)=0$

Du siehst sicher schnell, dass in diesem Fall sowohl C eins, als auch C zwei gleich Null sein müssen. So ergibt sich für die gesamte Biegelinie:

Ergebnis für die Biegelinie

Zusätzliche Berechnungen

Mit der Funktion w’= – $\varphi$ (x), erhältst du außerdem den Neigungswinkel. Im Detail sieht die Formel so aus:

$w'=\frac{F}{EJ}(lx-\frac{1}{2}x^2)$

Je nach Aufgabenstellung kann es sein, dass du auch noch die maximale Durchbiegung, bzw. Verdrehung berechnen musst. Dazu benötigst du diese zwei Formeln:

Maximale Durchbiegung: 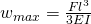$w_{max} =\frac{Fl^3}{3EI}$

Maximale Verdrehung: $\varphi_{max}=-\frac{Fl^2}{2EI}$

Damit haben wir die Funktion der Biegelinie bestimmt und die Aufgabe gelöst!

Beliebte Inhalte aus dem Bereich Festigkeitslehre

Intro Festigkeitslehre II

Biegung des geraden Balkens

Biegung des geraden Balkens - Einzellast

Biegung des geraden Balkens - Dreieckslast

Schubspannungen - Vollquerschnitte

Schubspannungen - Dünnwandig, offene Querschnitte I

Schubspannungen - Dünnwandig, offene Querschnitte II

Schubspannungen bei Torsion

Torsion - Verdrehwinkel

Eulersche Knickfälle

Eulersche Knickfälle - Übung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .