Schubspannung – Dünnwandig, offene Querschnitte I
Du willst wissen wie du die Schubspannung in Dünnwandigen Querschnitten berechnen kannst? Dann bist du hier genau richtig!
Inhaltsübersicht
Schubmittelpunkt und Schubspannung berechnen
Du hast auf Baustellen sicher schon mal einen Doppel-T-Träger gesehen. Diese Querschnitte nennen wir dünnwandig, offen. Wie du die Schubspannungen solcher Querschnitte berechnen kannst, zeigen wir dir jetzt.
Aber was bedeutet Dünnwandig überhaupt? Damit ist gemeint, dass die Profildicke deutlich kleiner ist also die Höhe oder Breite. Ein einfaches Beispiel ist ein dünnes Blech: 1mm dick aber mehrere Zentimeter hoch. Für den offenen Querschnitt kannst du dir ein Rohr vorstellen, das du einschneidest. Durch diesen Schnitt ist das Rohr offen geworden, da der Querschnitt nun nicht mehr durchgängig ist.
Nachdem du dir vorstellen kannst, worüber wir reden, wollen wir den Spannungsverlauf bestimmen. Das machen wir mit der im letzten Video bereits bestimmten Formel:

Zur Berechnung von offenen Querschnitten teilen wir den Querschnitt in Teilflächen ein und nehmen jede als einzelnen Vollquerschnitt an. Jeder Teilfläche wird dann eine Laufvariable s zugewiesen, die nur für diesen Abschnitt gilt. Zudem gehen wir von einer konstanten Profildicke je Abschnitt aus. So wird aus dem statischen Moment:

Damit erhalten wir dann für jeden Abschnitt den jeweiligen Verlauf.
Beispiel
Doch wie funktioniert das? Stell dir dazu ein liegendes U-Profil vor. Das U-Profil können wir in drei Flächen aufteilen: oben und unten die waagerechten und die senkrechte Fläche. Als nächsten ordnen wir der oberen Fläche die Laufvariable s eins zu, die rechts anfängt und an der Ecke aufhört. Für die zweite Fläche verwenden wir die Laufvariable s zwei, die genau die senkrechte Fläche durchläuft. Für die dritte Fläche verwenden wir die Laufvariable s drei, die von der Ecke zum Rand läuft. So können wir das Integral einfach aufteilen und sparen uns die komplexe Rechnung. Wir müssen jetzt nur aufpassen, dass wir keinen Sprung haben. Das heißt: das statische Moment, und damit auch die Schubspannung, müssen an den Ecken den gleichen Wert haben. Das hört sich zwar kompliziert an, aber im nächsten Video gehen wir dazu nochmal ein Beispiel durch.
Zum Schluss wollen wir noch den sogenannten Schubmittelpunkt betrachten. Doch was ist das schon wieder? Per Definition ist das der Ort, an dem die Querkraft angreifen muss, damit sich der Balkenquerschnitt nicht verdreht. Wenn du dir jetzt einen Balken mit einem T-Querschnitt vorstellst und den links oben mit einer Querkraft belastest, wird sich dieser verdrehen. Intuitiv würdest du in den Balken in der Mitte belasten, um das zu verhindern. Dabei hast du dann genau den Schubmittelpunkt gefunden.
Das Problem beim Schubmittelpunkt ist, dass dieser selten mit dem Schwerpunkt zusammenfällt und so immer zusätzlich bestimmt werden muss. Mit Hilfe der Definition können wir den Schubmittelpunkt durch ein Momentengleichgewicht finden. Das heißt das Moment, das die Querkraft erzeugt, muss genau dem Moment entsprechen, das durch die Schubspannungen erzeugt wird. Dabei ist der Punkt, an dem wir das Gleichgewicht bilden, egal.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Schubspannung berechnen
Zu Beginn definieren wir uns einen Abstand a, der den Abstand vom Schubmittelpunkt zum Punkt, an dem wir das Gleichgewicht bilden, darstellt. Diesen Abstand wollen wir schließlich wissen. Anschließend müssen wir noch die Kräfte aus den Schubspannungen bestimmen. Das erhalten wir mit Hilfe von:
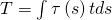
Als nächstes wollen wir das Momentengleichgewicht aufstellen. Die Kräfte aus den Schubspannungen zeigen dabei genau in die gleiche Richtung wie die Spannungen vorher. Für das liegenden U-Profil erhalten wir dann drei Kräfte: T eins, T zwei und T drei. Wir nehmen jetzt an, dass wir das Momentengleichgewicht an der oberen Ecke bilden. Hier Fallen die Momente der Kräfte T eins und T zwei weg, da diese genau durch den Punkt verlaufen. Das Momentengleichgewicht ergibt sich damit einfach zu:

Anschließend muss die Formel nur noch nach a umgeformt werden zu:
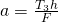
Im nächsten Video erklären wir dir das nochmal detaillierter anhand eines Beispiels.
So kannst du für jeden beliebigen offenen Querschnitt den Schubspannungsverlauf und den Schubmittelpunkt bestimmen. Bis bald.
