Schubspannung – Dünnwandig, offene Querschnitte II
Du willst wissen wie du die Schubspannung in Dünnwandigen Querschnitten berechnen kannst? Dann bist du hier genau richtig!
Inhaltsübersicht
Schubmittelpunkt und Schubspannung berechnen
Zunächst frischen wir noch einmal die Grundlagen auf. Allgemein gilt für einen Balken unter Querkraftlast:

Dabei ist S das statische Moment:

Und b entspricht der Breite eines Vollquerschnitts. Oft betrachten wir dünnwandige, offene Querschnitte. Das heißt die Profildicke ist deutlich dünner als die restlichen Abmessungen.
Für dünnwandige, offen Profile bestimmen wir den Schubspannungsverlauf nicht als Ganzes, sondern für die einzelnen Flächen, wobei wir für jede Fläche eine Laufvariable s definieren. Dabei wird aus der Dicke des Vollquerschnitts die Profildicke t jedes Abschnitts:

Dann gibt es noch den Schubmittelpunkt. Dieser ist definiert als der Punkt, in dem die Querkraft angreifen muss, damit sich das Profil nicht verdreht. Also der Punkt, an dem die Summe aller inneren und äußeren Momente gleich Null ist. Diesen ermitteln wir dann mit einem Momentengleichgewicht. Wobei wir aus den Schubspannungen die jeweiligen Kräfte erhalten mit:
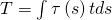
Beispiel
Nachdem wir das aufgefrischt haben, schauen wir uns einen Balken an, der am Ende im Schubmittelpunkt mit einer Querkraft F gleich 2000 Newton belastet wird. Das heißt wir haben keine Verdrehung, und der Querkraftverlauf ist konstant. Der Querschnitt ist ein einfacher T-Träger. Der Träger hat die Höhe h gleich 110 Millimeter. Der rechte Teil des T hat die Breite b eins gleich 60 Millimeter und der linke Teil des T hat die Breite 40 Millimeter. Das Koordinatensystem legen wir in den Schwerpunkt. Dieser liegt 28,81 Millimeter unterhalb des Kreuzes und ist um 4,76 Millimeter nach rechts verschoben, wobei die y-Achse nach links und die z-Achse nach unten zeigt. Die Profildicke ist überall konstant bei t gleich zehn Millimeter.
Mit den Abmessungen erhalten wir ein Flächenträgheitsmoment J zwei zwei von 2,6936 mal Zehn hoch sechs Millimeter hoch vier. Wir können annehmen, dass der Träger dünnwandig ist und wollen jetzt zunächst den Schubverlauf und anschließend den Schubmittelpunkt bestimmen.
Für den Schubspannungsverlauf teilen wir den Träger in drei Abschnitte ein:
- oben rechts, mit s eins von Null bis b eins,
- oben links, mit s zwei von Null bis b zwei, und
- den Steg, also die senkrechte Verbindung, mit s drei von Null bis h,
Dabei fangen die Laufvariablen s eins und s zwei außen an. S drei fängt oben bei Beginn des Steges an. Da wir erst am Ende mit Zahlen rechnen möchten, nennen wir den Abstand des Schwerpunkts zum Kreuz z S.
Als nächstes bestimmen wir für jeden Bereich erst den Verlauf des statischen Moments und anschließend daraus den Schubspannungsverlauf. Bei der Berechnung des statischen Moments erhalten wir immer eine Integrationskonstante C, die wir dann mit Hilfe von Randbedingungen bestimmen.
Für Bereich eins gilt, das z konstant bei  ist. Damit erhalten wir für das statische Moment im Bereich eins:
ist. Damit erhalten wir für das statische Moment im Bereich eins:

C eins kriegen wir heraus über die Randbedingung, dass das statische Moment am Rand gleich Null sein muss. Damit ergibt sich C eins auch zu Null.

 bestimmen kannst, dann schau dir doch einfach unser
bestimmen kannst, dann schau dir doch einfach unser